Teacher: put these few lines on the board for one of those towards-the-end-of-teerm lessons when people are late turning up to class: Or a lesson where you don’t mind the noise, but you really have to get something else done, like those reports….
Choose a two digit number. Square each digit; add the results and you will have another digit number (most probably still of two digits). Repeat the process. And repeat the process. And repeat… Explore.
Example: choose 88; 8²+8²=128; 1²+2²+8²=69 and so on, through 115, 27, 53, 34, 25, 29, 85, 89, 145, 42, 20, 4, 16, 37, 58, 89, 145,..... and you realise that you’ve seen some of these before. this is a chain of ten to the loop of eight.
Example: choose 70; you get 49, 97, 130, 10, 1 and it stops.
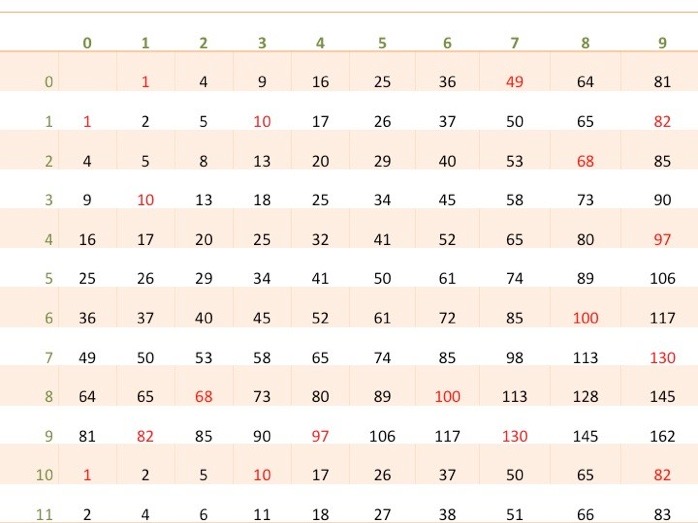
I made a table¹ showing what the next number will be, which I would suggest could be formed by group-work or homework, depending on the ability and excitement of the class. My Year 10 class lost interest almost immediately, while the year 8s and 9s enjoyed playing with this – but it was the last half-day with lessons in the term.
Obviously 79 produces the same results as 97, but 79 has, upstream, no digit combination that creates a 79 [test by deducting each square up to halfway to see if any are squares; 78, 75, 70, 63, 54, 43] ²
The green labelling gives a two digit number, first digit row, second digit in column (but it doesn’t matter which is which); the black and red then gives the resulting number from each two digit number. The red is used for the ‘head-to-unity’ group.
I drew a swirling pattern with the circuit in the middle and the chains drifting off, like a galactic drift. It is hard to make this copy across.
Play with this a little. Or a lot. I work quickly and I’ve filled an hour easily each time I’ve forgotten what happens.
DJS 20130627
...more to come when I’ve made the next diagram work (better). Perhaps never…, or when not only have the cows come home, but someone has written to me about this….
Revisiting this in 2017, it would be smart to explore upstream. Take the loop 4-16-37-58-89-145-42-20-4 for example. Upstream of the 4 is 2; upstream of that is 11, upstream of that is 113, upstream of 113 is 78. Showing that 78 has nothing upstream of it is a different problem. Call 78 a source; if it has nothing upstream then subtracting successive squares {1,4,9,16,25,36} will produce only remainders that are not square {77, 74, 69, 62, 53, 42}. There is no point going further than the halfway point, 39. These should be coloured differently on the table. One way to produce the sequence {77,…} is to subtract successive odd numbers from 78. Thus I discover that 87 is also a source, since 87-9=78, a known source.
The statement in blue is only true for two-digit numbers: 14 looks like a source, but is reached from 123 (and combinations of those digits). 78 could be reached from many places, but one such would be 11175.
We have two distinct sets, those that devolve to unity and those that join the loop.
A list of sources would only be valid if made conditional with statement such as 'cannot be created from a smaller number’, however indirectly. Looking at the numbers from 70 to 80, results appear to be:
70->1, 71->89 loop, 72->145 loop, 73->58 loop 74->37 loop, 75->37 loop, 76->89 loop, 77-> 78->4 loop , 79->1.
Looking instead upstream, at the smallest number that can form these same numbers:
356->70, 1356->71, 66->72, {166, 83, 38}->73, {57, 75, 138}->74, 157->75, 266->76, 238->77, 257->78, {1257, 1138}->79,
I had a little look at doing the same thing with chains of cubes. the numbers 370 and 371 are sinks, since the sum of their cubes is 370 and 371 respectively, numbers 3 to 9 link to 371, as do 12 to 15. Other sinks are 1, 407 and 153. I found some loops, too, which I will reference by the lowest number in the cycle: 55, 160, 919, 136,
You might investigate 177, which I think devolves to 153 eventually.
I will respond to mail on this. My spreadsheet seems to work fine.
1 I discovered that putting tables into iWeb is quite as hard as I feared long ago. The solution used was to save Excel tables in Powerpoint, with zero border, filing the powerpoint slide, and then save as pictures, copying the jpeg files into one’s webpage creation software, in this case iWeb at the time. The colour I used in the excel file did not copy to Powerpoint.
2 78, 75, 70, 63, 54, 43 could of course become downstream of far longer numbers, 54 could be adjacent to something as low as 127, 75 to 555, 63 to 255 an (interesting coincidence of 2ⁿ-1 there) or to 1237, 70 to 1128 and 43 to 11126. Thus 79 might appear to be a source, but if you look upstream then it can come from, taking 79=25+54 for example, then upstream of 79 would include the mix of 5 and 127 (25=1=4+49=79), so teh numbers immediately upstream of 79 includes 1257 (and other digit orders, of course, but I picked the earliest integer).