The CIE Syllabus says:
(i) formulate hypotheses and apply a hypothesis test concerning the population mean using a small sample drawn from a normal population of unknown variance, using a t-test
(ii) calculate a pooled estimate of a population variance from two samples (and do calculations too)
(iii) formulate hypotheses concerning the difference of population means, and apply as appropriate: a) a 2-sample (pooled) t-test, b) a paired sample t-test c) a test using a Normal distribution - including choosing the right test.
(iv) determine a confidence interval for a population mean based on a small sample drawn from a normal population of unknown variance, using a t-distribution
(v) determine a confidence interval for a difference of population means using a t-distribution or a Normal distribution as appropriate.
We have established that the means of samples from a distribution are clustered as
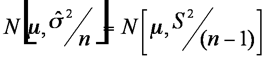
noting the use of the ‘hat’ on the sigma. Our two assumptions are that the sample is random and that the variable is normally distributed (the parent population is assumed to be Normal) and that if we look at two samples then the items could be paired or pooled.
Paired test: We have a set of n differences for X in two conditions. Call this variable U.
Then the sample mean U can be found, as can the sample variance S2. We can estimate
![]()
using the relationship
![]()
We recognise that the degrees of freedom is one less than n, so provided that U is distributed normally in the population then
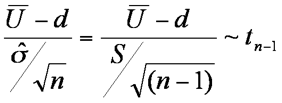
Unpaired test: We have two sets of data, X1 and X2 taken from a parent population assumed to be Normally distributed. The samples sizes are n1 and n2, the sample means are
![]()
and
![]()
(sorry,means of ‾X1 and ‾X2)
while the sample variances are S12 and S22 .
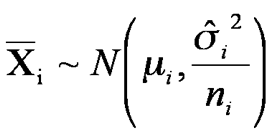
Then
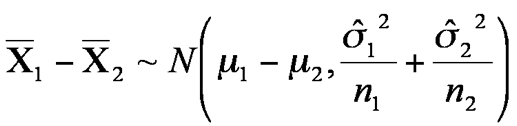
and
adding variances because X2 is multiplied by -1.
But the difference of the means should be zero,
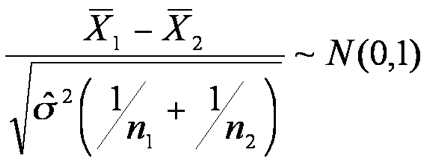
So the standardised distribution is
but we use the t-distribution because the samples are relatively small, with the number of degrees of freedom n1+n2-2. We must be careful with our alternative hypothesis to distinguish between the one and two tail test; similarly we must be aware which figures our data tables give, one or two tailed. A diagram helps dramatically to show that of the test statistic is bigger than the tabulated figure, we will reject H0, the null hypothesis.
It was very difficult to make this even this bad to read. Short of using LATEX to write maths scripts, I don’t know what else to do. Even this is basically imported picture files
At all times you are assuming that your samples are unbiased and that the underlying population is Normally distributed.
1 The heights of a random sample of Gaoxin policemen were measured as 176, 179, 179, 180, 181, 183. The heights of a similar sample of eleven in Xi’an city gave Σy= 1991, Σ(y-)= 54, where all heights are measured t the nearest centimetre. Test, at the 5% level, whether the city policemen are shorter than those in Gaoxin. Assume that both forces have a normal distribution of height and that they have a common population variance.
2 A large number of tomato plants are grown under similar controlled conditions. A new fertilizer is applied to half the plants chosen randomly and the others are treated with the standard fertilizer. Random samples of a hundred are chosen from each half and records are kept of the weight of tomato collected from each plant. Both samples can be treated as being large samples from a normal distribution with a common variance. The standard treatment produces Σx= 990, Σx2=10079. The new treatment produces Σy= 1030, Σy2=11046.
a.Obtain a 96% symmetric confidence interval for the mean mass of the ‘new’ crop.
b.Calculate a pooled estimate of the variance
c.Assuming that the new fertilizer cannot be any worse than the old one, and stating your hypotheses clearly, test at the 3% level the suggestion that the new fertilizer implies a greater crop mass.
3 There is a theory that the foot size is connected to intelligence, on the grounds that both are indicators of good genes and feeding. Sampling first year undergraduates at Oxford University by measuring feet to the nearest cm, I obtained these figures:
Length 24252627282930
Frequency 1239651
a. Find the sample mean and the unbiased estimate of the population variance.
b. Calculate a 96% confidence interval for the mean length of foot for such people.
A collection of 48 similar students from Oxford Brookes University is also measured. We can assume that these students are of medium intelligence. The mean foot length is 26.6cm and Σ(y-)= 123.20. If we assume that the two samples are drawn at random from independent normal distributions with a common variance, then
c. Obtain an unbiased two-sample estimate of this common variance
d. Test the genetic theory at the 1% significance level, clearly stating your hypotheses. Make a comment on the theory in the light of your test, including discussing how your conclusion changes with significance level.
4 A machine is used to fill bags with powdered ink and a random sample of twenty bags taken from a week’s production gave a mean mass of 499.1g and a std dev (r.m.s.d.) of 0.63g. A week later a sample of 25 bags gave 500.2g and 0.48g. Stating the conditions you require as assumptions, test
a. whether the mean has changed significantly during the week, and, both at the 5% level,
b. whether the mean in the second week could be 500g.
1 Gaoxin mean 179.67, S2=4.556 Xian: 181, 5.422. test t is -1.13. Accept H0.
2 4.41, (9.87, 10.73), 3.61, z = 1.49.
3 Mean, Variance 2.00. (26.77, 27.39) z= 1.97 Accept H0.
4 |t| = 6.496, Yes; t= 2.041, Yes