1 A uniform thin rod FH of mass M has length 2a and its centre of mass at G. Its moment of inertia is designated by Φ.
Show that the Φ about an axis
(i) perpendicular (at right angles, normal) to the rod through G is ⅓ Ma².
(ii) at an angle of θ to the rod through G is ⅓ Ma²sin² θ
The centre of rotation is moved to position P on the rod at a distance r from G so that the inertia is now Φ= ½ Ma². Quoting any theorems used, find r when rotation…
(iii) remains as (i), normal to the rod
(iv) remains as (ii), at an angle to the rod
(v) for the last case find the range of r & the corresponding range for sinθ.
2(i) A uniform rod of length 2ℓ and mass M is suspended from one end so that it can rotate in the plane of the rod. State the moment of inertia, Φ.
(ii) A point mass of size M is suspended from a light string such that the inertia is the same as that of the rod just described. Find the length of the string. This is known as the radius of gyration.
(iii) A right angled 3-4-5 triangle is constructed from 12 length units of a uniform wire. This is to be suspended from the most acute (4-5) apex and rotated about an axis perpendicular to the plane of the triangle. Find Φ.
(iv) A lamina identical in mass and shape to the triangle in (iii) is suspended and rotated in the same way. Find Φ.
(v) Comment on the centre of mass of these two shapes.
3 The rod of length 2ℓ from question 2(i) has a particle of mass 2M added to the lower end. The rod is pivoted about a point R, ℓ/3 from the upper end so the rod acts as a pendulum.
Find (i) the moment of inertia, Φ (ii) the radius of gyration
4(i) Express cos4θ as a series in cos nθ. Integrate cos4θ.
(ii) Find the moment of inertia, Φ, of a semicircular lamina about the axis that forms the base diameter.
iii) Determine Φ for the axis of symmetry.
(iv) Find Φ for the axis normal to the plane through the centre and
(v) normal to the plane through the end of a diameter.
5(i) Use calculus to calculate the moment of inertia for the 3-4-5 triangular lamina in through two other axes so as to check your answer to 2(iv)
(ii) Do the same thing for the rods in 2(iii) so that you are satisfied with the answers.
6(i) Find the moment of inertia of a solid cone radius r and height h about its axis of symmetry.
(ii) Hence find the Φ about an axis normal to the symmetry and through the apex of the cone.
(iii) Do the same thing for a conical shell
(iv) Add a base to the cone and find the inertia for the axis along the line of symmetry.
7 A semicircular framework is made from uniform heavy wire, of diameter 2a.
Find the moment of inertia about an axis
(ii) through the centre and normal to the plane of the semicircle
(iii )along a tangent parallel to the diameter and in the plane
(iv) through the line of symmetry of the shape, in the plane
Use the three answers to check each other, using the parallel axis theorem. If you used it already, rework that part of the answer from first principles.
8 A yoyo consists of two uniform disks each of mass m and radius 4a, and a small cylinder of mass 3m and radius a, between the two disks. The three have common axes of symmetry. A light inextensible string is wrapped around the cylinder and fastened at one end to the cylinder; the other end is held firmly at a fixed point. The yoyo is projected downwards at a speed of 4 √(ag) and the string, as it unwinds, becomes vertical. Find the speed of the centre when a length of 126a has unwound.
By the end of this page you should have realised that the inertia has a minimum when the axis of rotation passes through the centre of mass, which is why mistakes are made with the parallel axis theorem. The equivalent error with the perpendicular axis theorem is to forget that the ‘other’ two inertia values must be in the plane of the body - so it must be a lamina.
1(iv) the form is r² = a cosec²θ – b and you might sketch this curve for practice.
2(iii) Rods 10 Mℓ² (iv) Lamina 19/2 Mℓ²
3 r = √19 ℓ/3 4(i)1/8 (cos 4θ +4cos 2θ+3) first part is relevant, or should be.
5 the smaller values are 1½ Mℓ² but not 27/16 Mℓ²
6 (ii) 3M/20 (r²+4h²) (iii) ½ Mℓh (iv) ½ Mℓ²
7 (i) and (iii) below are correct
![]()
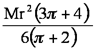
8 6√(2ag) is correct; the yoyo begins spinning after projection. This question from a Bostock & Chandler Mechanics 2., end of Chapter 11.