Choose a two digit number. Square each digit; add the results and you will have another digit number (most probably still of two digits). Repeat the process.
Example: choose 88; 82+82=128; 12+22+82=69 and so on, through 115, 27, 53, 34, 25, 29, 85, 89, 145, 42, 20, 4, 16, 37, 58, 89, 145,..... and you realise that you’ve seen some of these before. this is a chain of ten to the loop of eight.
Example: choose 70; you get 49, 97, 130, 10, 1 and it stops.
I made a table¹ showing what the next number will be, which I would suggest could be formed by group-work or homework, depending on the ability and excitement of the class. My Year 10 class lost interest almost immediately, while the year 8s and 9s enjoyed playing with this – but it was the last half-day with lessons in the term.
Obviously 79 produces the same results as 97, but 79 has, upstream, no digit combination that creates a 79 [test by deducting each square up to halfway to see if any are squares; 78, 75, 70, 63, 54, 43] ²
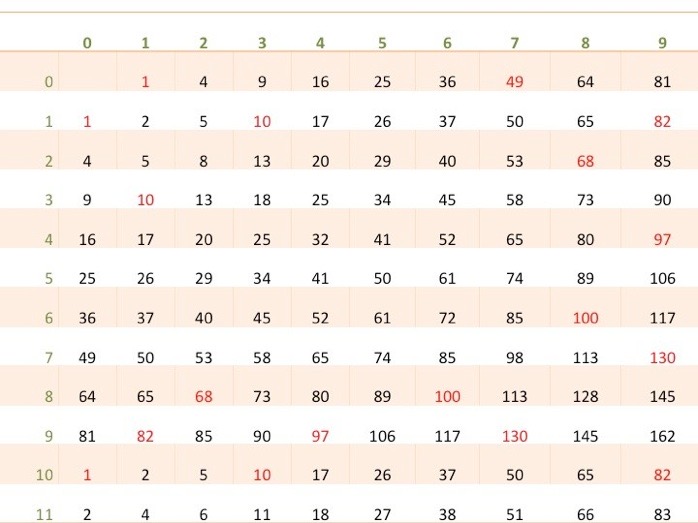
The green labelling gives a two digit number, first digit row, second digit in column; the black and red then gives the resulting number from each two digit number. The red is used for the ‘head-to-unity’ group.
I drew a swirling pattern with the circuit in the middle and the chains drifting off, like a galactic drift. It is hard to make this copy across.
Assuming that you’re going to go play with this a little, let....
more to come when I’ve made the next diagram work (better). Perhaps never...
DJS 20130627
1 I discovered that putting tables into iWeb is quite as hard as I feared long ago. The solution used was to save Excel tables in Powerpoint, with zero border, filling the slide, and then save as pictures, copying the jpeg files into iWeb. The colour I used in the excel file did not copy to Powerpoint.
2 78, 75, 70, 63, 54, 43 could of course become downstream of far longer numbers, 54 could be adjacent to something as low as 127, 75 to 555, 63 to 255 an (interesting coincidence of 2ⁿ-1 there) or to 1237, 70 to 1128 and 43 to 11126.