1 Establish the rank of the matrix A
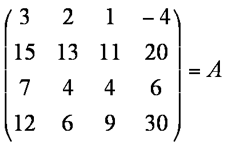
and reduce it to echelon form, E.
Given that Ax = ( 6 30 11 15 )
show that x = x0+λe is a valid form for vectors x0 and e and a variable, λ. Show that there are no points in the positive quadrant.
[Helpful check: e = (…, …, …, 27) ]
2 Use induction to show that MISSING !!!!!
and find three prime factors of S100.
3 Point P is 3i – 4j + 5k,
Q is 2i +3j –k,
R is –1i + 3j +k and
S is 10i + 9j -8k.
The line ℓ1 includes P and Q,
line ℓ2 goes through S parallel to OP and
line ℓ3 goes through R, perpendicular to both ℓ1 and ℓ2.
(i) Find an equation for ℓ3
(ii) Find the shortest distance from S to ℓ3. Find also the foot of this
perpendicular in the form 1/43 (p, q, r)
(iii) Find the equation of the plane π3, that includes Q and ℓ3.
(iv) Find the distance from S to π3.
4 Find the eigenvectors of the matrix M
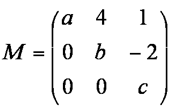
Find P and D such that (M-kI)ⁿ=PDP-1 where I is the identity matrix, k is a constant scalar and n is a positive integer.
5 (i) Prove that the inertia of a rod length 2a rotated around its centre of mass along an axis perpendicular to the rod is ⅓ Ma².
Find the inertia when it is rotated
(ii) around an end so that the rod is in the plane of rotation
(iii) around a point along the line of the rod, but 2a from the centre
(iv) by suspension from the middle of a light string of length 2λ, connected to the ends of the rod so that the rod remains in the plane of rotation.
6 The continuous random variable X has a probability function
f(x) = k e q-px for x≥3. f(x) is otherwise zero.
(i) Find an expression connecting p,q & k.
While p = k, (working entirely in terms of p)
(ii) Calculate the probability distribution
(iii) Write an expression for the median
(iv) Find expressions for the expectation and variance.
7 There are five points found for the curve y=f(x)
(i) Sketch possible curves that will fit the following cases:
a) the linear pmcc is close to 1 (product moment correlation coefficient )
b) the pmcc is close to zero
The table shows the age, x, and %body fat, y, for a random sample of ten adults
x 23 27 39 41 45 49 53 54 57 61
y 18.9 28.7 40.9 33.9 38.6 35.8 43.9 39.7 40.8 46.5
(ii) Calculate the linear pmcc for the sample. They are Americans. Comment.
(iii) To test whether body fat increases with age, calculate a rank correlation coefficient and test it at the 5% level. State your conclusions. Clearly.
8 Differentiate x(1+x²)-n and show that this is also
2n(1+x²)-n-1 – (2n-1) (1+x²)-n. Check index !!!!
Hence show
It is given that . 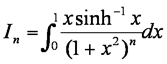
Hence show that, while n ≠ 0.5, 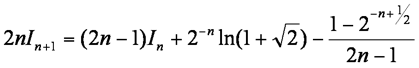
and deduce that MISSING EXPRESSION !!!!!
2 I developed this formula myself. I think the even powers have curious formulae and the odd powers are predictable. N(N+1) (2N+1) seem to be common factors.
3(i) I think the direction vector of ℓ3 could be written as (a b c) where b² + ac +18 = 0
(ii-iv) I found I wanted roots of 579, 95106 and 3038. The 1/43 didn’t help and should have been something else; these questions are hard to write with ‘nice’ numbers, which may explain why at least one question has been re-used.
6 The CIE examiner uses probability distribution, F(x) when he means cumulative probability distribution. Last reminder ! The target questions go on to define related functions….
7 The US population suffers from obesity. It might well be a bimodal distribution, very fat and very thin. Contributing factors are too much money. too much ‘fast’ food, not enough exercise and a social acceptability of extreme size. Being slim becomes an attribute of being well off, unlike other cultures where success is echoed by a matching weight. Or overweight. Obesity leads to type II diabetes and other disorders, some of which are extrremely unpleasant - and these usually shorten one’s life.