This sheet looks at the Pure we haven’t done much work on.
1 The plane A has vector equation
r= i+7j-3k + (i-2j+2k + µ(2i-3j+2k
The points P & Q, not in the plane have position vectors 4i+5j+7k and 10i+8j +k respectively, and the line l1, which passes through P and Q, meets plane A at the point R. Find the position vector of R. [4]
The line l2 is perpendicular to l₁, passes through R and lies in the plane. Find the direction of l₂. [5]
2 The curve C has equation y = a/x + b/x² where a and b are constants such that a>0 and b≠0. Show that C has exactly one stationary point and find its co-ordinates in terms of a and b [4]
On separate diagrams, draw a sketch of C for b>0 and for b<0. In each case mark the intercepts (where the line meets an axis) [6]
Use your diagrams to show that there are positive values for m for which the equation
mx³ – ax – b = 0 has three real roots [4]
3 The set S consists of all numbers of the form a + b√5, where a and b are integers. Show that
a) S is closed under addition and multiplication [2]
b) there is an identity in S for addition and one for multiplication [2]
c) not every element of S has an inverse with respect to multiplication [2]
The conjugate of x = a + b√5 is xc = a - b√5. The relation я is defined on S by:
[(a1 + b1√5) я (a2 – b2√5)] [a1b1 = a2b2 (mod 5)]
d) Show that я is an equivalence relation, that is, that the relation is symmetric, reflexive and transitive. [3]
e) Determine the subset T of S such that, for each element x in T, xяq and xc2+q2=0 (mod 5), where q = 1 + 2√5 [5]
4 Find the general solution of the differential equation y” + 2y’ +2y = sin3x where y’ means the 1st differential with respect to x. [5]
Hence show that y = psin3x+ qcos3x, for large positive x, and expressing p and q as rational numbers, irrespective of the initial conditions. [2]
5 Write a definition of sinh x.[1]
Write the equivalent equation to these circular function identities and equations using the hyperbolic functions, developing them from first principles.
sin² x + cos² x = 1 [2]
sin2x = 2 sinx cosx [2]
cos 3x = 3 cos x + 4 cos³x [2]
6 The curve C is defined parametrically by x = sinh t, y = tanh t for real t. The section of C that joins the origin to the point where t=ln2 is rotated about the x-axis. S is the integral
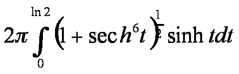
Show that the area of the surface generated is given by S as above [don’t attempt the integral] [4]
The mean value of z-3(1+z6)1/2 over the interval 1≤z≤5/4 is denoted by M. By finding the connection between z and t, show that S= M π/2 [4]
7 The system of equations 2x+4y+z = 1; 3x+5y=1; 5x+13y+7z=4 has a solution of the form a + λb where a and b are vectors in three dimensions. Use a matrix method to find the solution.
8 The integral In is defined for n≥1.
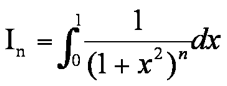
By considering the differential of the expression shown x (1+x²)-n
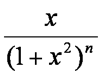
show that 2nIn+1 = (2n-1)In+2-n [4]
Evaluate I5 exactly. [3]
9 Sketch the curve r – θ = 2π for |θ| ≤ 6π [4]
Sketch separately, and for the same range of values as above, the similar curves
3r – θ = 2π and r – 4θ = 2π. [4]
10 The pair of simultaneous differential equations, dx/dt = 2x+4y and dy/dt = x-y are not readily solvable. However, you can plot the tangent field for |x|<5 and |y|<5. By investigating the value of dy/dx for various values of x and y, sketch the solution sets for the pair of equations. Try to find the (two) lines for which dy/dx = mx. Try to put arrows on your lines indicating increasing values of t. [6]
1 w93_p1_q11
(-2, 2, 13); (20, -24, 8) or(); (5, -6, 2)
2w93_p1_q1 (-2b/a, -a2/4b)
3w94_p1_q7
4w93_p1_5(a)
-7/85, -6/85
5DJS
6w93_p1_4(a)
Is not as hard as it looks.
z = cosh t
7Cohn Linear Equations Ex IV Q9
½(-1, 1, 0) + λ(5, -3, 2)
8Specimen 1992 P1Q7(a)
9 developed in class, Dec’07
10 MEI Diff Eqns (M4, once) example Qn