
Exercise:
1) If Charlie put 5% of his £30k salary into a pension every year for 25 years and his employer puts 9% similarly, how much would he expect the annual income to be on collecting the pension? Assume little change in real terms; assume inflation is included in the investment return; assume tax does not apply. Choose an investment return, such as 5%
2) Repeat, but assume £28k and 4%
3) Repeat but assume £25k and 3%.
I could, perhaps should, put this in the Other Subjects section beside Pension and Sinking Funds. For those few who read my stuff, I’ll let it sit here for a while.
DJS 20141020
I shall assume you built a formula, and I shall use these symbols:
A = Amount produced by the fund just before collecting it as pension;
S = annual salary - so b = 0.14 S / 12 is paid monthly. S=3x104, b= 350
= annual interest rate on the investments, where in practice the real growth is the excess over inflation.
j=1+𝑰/12, the interest increase per month, so 3% per annum puts j=1.0025
N=years of pension, in this case N=25. n=12N, months of pension contribution.
Go away and think about this. Scratch away on paper. Come back tomorrow.
One version of an answer comes from the page on Pensions. I quote:
Bertha’s Total after ten years = b* (j120 - 1) / (j-1) = b *(12/i)* [(1+i/12)120 -1]
so in this case
Charlie’s Total after 25 years = b* (j300 - 1) / (j-1) = b *(12/i)* [(1+i/12)300 -1]
Using j=1.03 and b= S/12 =350 gives the grand total of 156103 to the nearest integer.
At S=30k and 𝑰=5%, A= 208 428
At S=28k and 𝑰=4%, A= 167 949
At S=25k and 𝑰=3%, A= 130 086.
Okay so now we have a fund from which to pay pension, or at least in theory we do. In practice, what is paid out is based a different calculation based on years of service and average expected life remaining, paid out of the collected accumulated funds of all contributors. What I’m doing here is looking at the prospect of what was originally sold to me, the idea that my money goes into a pot, from which I will fund my retirement. That is something topical, as the government is looking at saving itself a ton of money by doing exactly that. Since we’re basically stupid, we’d mostly die with a load of money left in the pot and I expect the state to claw much of that back, either by taking it, or taxing the residual estate. Financiers are invited to criticise my simple modelling and to proffer something ‘better’, meaning more complicated but closer to what actually happens.
Suppose we have amount A from which to pay a pension. Imagine I’m going to live another 30 years or so; ignoring inflation, in the sense that the remaining investment will grow to cover that, how much is the annual pension?
Let’s call the annual pension P, the remaining life L years. Again, go do some sums on your own and come back to this, please.
I’m thinking one crude way to look at this is simply treat the Amount as producing interest and just extract that. Multiply A by 𝑰. so A=£200k, 𝑰=5% => P= £10 000.
A slightly smarter way is to pay interest and a smidgen of capital so the fund has nothing left after 30 years. This is the reverse of a mortgage, where a regular sum is put into the fund so as to owe nothing at the end of the cycle. Using the amortisation calculation from here, I get A=£200k, 𝑰=5% => P= £12 885. That is quite an improvement. If Charlie has control of his funds and expects to live only ten years past retiring, he’d be looking at P= 25k.
In the financial climate we have at the moment, 3% is a good return, maybe very good. Repeating the last two calculations:
A=£200k, 𝑰=3%, L=30 => P= £10 118
A=£200k, 𝑰=3%, L=10 => P= £23 175
Now, forget Charlie and do this for your own case. You will have committed how many years? You expect what return? How does that affect what you put into a pension? Are there some better things you could do with the money?
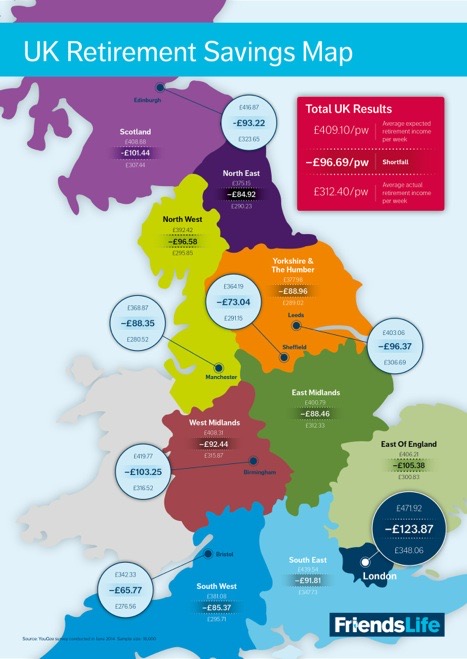
Now look at this diagram I found when researching on devolution, essay 151, and wonder what calculation needs to be done by you so that you take some action.
Diagram showing retirement savings Savers expect on average to be £97 a week short when retirement savings are compared with the expected outgoings in retirement, according to major research from Friends Life.
The insurer looked at the savings behaviour of 18,000 consumers in England and Scotland. It found that although 58 per cent hold some form of pension, and almost a quarter (23 per cent) are saving as much as they can afford into their pension, overall, the average total value of retirement savings (£312 a week) will not cover expected living and housing costs (£409 a week).
Far too many people do maths only under duress and those same people do not do the (usually quite simple) maths that affects their lives.
E.g. It’s eleven thirty and I’m for bed, so 8 hours means... oh dear I’ll be late tomorrow (or short of sleep); why didn’t I think of that sooner?
E.g. I’m out walking in the hills and I have a map. If I’ve come this far in that time, then I’ll be there at this time. That rate means I’ll be finished at this (unacceptable) time, so I need to go faster or change the route, don’t I?
E.g. I did those pension calculations but it’s a long time in the future, so there’s no need to worry about it now, is there?
If maths isn’t useful, why are we bothering with it? So many school-kids feel that way, about much of their lives, hence the escapism. Blaming all of school on exams makes the whole of school largely self-serving: we go to school because there are exams; good results mean a better life?
There is a strong correlation between better education and increased lifelong earning. perhaps I should write about that, too?
DJS 20141020
edits 20150109
