
I fondly remember finding a notice on the board in the Mathematical Institute, probably in my first year at Oxford, explaining how to catch a lion in the desert. In writing the previous essay 197 I started writing a footnote about Occam’s razor and distracted myself enough to write this too.
I particularly liked Schrödinger’s version, which simply placed a cage in the desert with an instruction to occasionally go look to see if the lion had arrived yet. See a 2016 version, which you might view as a test to see if you’re a scientist—if you are, they’re funny. And if they’re funny, you are a in some way a scientist. The computer science (necessarily post-1970) suggestions had me grinning, but we could add The Apple Approach: “Find your back-up OS X disks. There’s Lion”. And Mountain Lion. Or, “log on to the net. Download Lion.” Desert unnecessary. Other suggestions from Columbia. I like the Shakespeare method but most of these are good and there is little in common with the other set. Also here, which explains the original source as being H Petard, 1938. Now there’s a seminal paper.
H Petard, I found, is a pseudonym (hoist by one’s petard, indeed) for Ralph P Boas, Jr, 1912–92, a mathematician after my own heart. Do read the wikipedia entry linked here. If you have come across the Pondiczery theorem, you’ll love it.
So let us collect them here: In Blue is a copy of the original from 1938, found here and here
‘A Contribution to the Mathematical theory of Big Game Hunting’, H Pétard, Princeton, NJ — The American Mathematical Monthly, Aug.-Sept. 1938, pp. 446-447.
This little known mathematical discipline has not, of recent years, received in the literature the attention which, in our opinion, it deserves. In the present paper we present some algorithms which, it is hoped, may be of interest to other workers in the field. Neglecting the more obviously trivial methods, we shall confine our attention to those which involve significant applications of ideas familiar to mathematicians and physicists.
The present time is particularly fitting for the preparation of an account of the subject, since recent advances both in pure mathematics and in theoretical physics have made available powerful tools whose very existence was unsuspected by earlier investigators. At the same time, some of the more elegant classical methods acquire new significance in the light of modern discoveries. Like many other branches of knowledge to which mathematical techniques have been applied in recent years, the Mathematical Theory of Big Game Hunting has a singularly happy unifying effect on the most diverse branches of the exact sciences.
For the sake of simplicity of statement, we shall cofine our attention to Lions (Felis leo) whose habitat is the Sahara Desert. The methods which we shall enumerate will easily be seen to be applicable, with obvious formal modifications, to other carnivores and to other portions of the globe. The paper is divided into three parts, which draw their material respectively from mathematics, theoretical physics, and experimental physics.
The author desires to acknowledge his indebtness to the Trivial Club of St. John's College, Cambridge, England; to the M.I.T. chapter of the Society for Useless Research, to the F. o. P., of Princeton University; and to numerous individual contributors, known and unknown, conscious and unconscious.
1. THE HILBERT OR AXIOMATIC METHOD.
We place a locked cage at a given point of the desert. We then introduce the following logical system.
AXIOM I. The class of lions in the Sahara Desert is non-void.
AXIOM II. If there is a lion in the Sahara Desert, there is a lion in the cage.
RULE OF PROCEDURE. If p is a theorem, and "p implies q" is a theorem, then q is a theorem
THEOREM I. There is a lion in the cage.
2. THE METHOD OF INVERSE GEOMETRY. We place a spherical cage in the desert, enter it, and lock it. We perform an inversion with respect to the cage. The lion is then in the interior of the cage, and we are outside.
3. THE METHOD OF PROJECTIVE GEOMETRY.
Without loss of generality, we may regard the Sahara Desert as a plane. Project the plane into a line, and then project the line into an interior point of the cage. The lion is projected into the same point.
4. THE BOLZANO-WEIERSTRASS METHOD.
Bisect the desert by a line running N-S. The lion is either in the E portion or in the W portion; let us suppose him to be in the W portion. Bisect the portion by a line running E-W. The lion is either in the N portion or in the S portion; let us suppose him to be in the N portion. We continue this process indefinitely, constructing a sufficiently strong fence about the chosen portion at each step. The diameter of the chosen portions approaches zero, so that the lion is ultimately surrounded by a fence of arbitrarily small perimeter.
5. THE "MENGENTHEORETISCH" METHOD.
We observe that the desert is a separable space. It therefore contains an enumerable dense set of points, from which can be extracted a sequence having the lion as limit. We then approach the lion stealthily along this sequence, bearing with us suitable equipment.
6. THE PEANO METHOD.
Construct, by standard methods, a continuous curve passing through every point of the desert. It has been remarked(1) that it is possible to traverse such a curve in an arbitrarily short time. Armed with a spear, we traverse the curve in a time shorter than in which a lion can move his own length.
7. A TOPOLOGICAL METHOD.
We observe that a lion has at least the connectivity of the torus. We transport the desert into four-space. It is then possible (2) to carry out such a deformation that the lion can be returned to three-space in a knotted condition. He is then helpless.
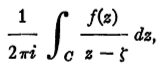
8. THE CAUCHY, OR FUNCTIONTHEORETICAL, METHOD.
We consider an analytic lion-valued function f (z). Let ζ be the cage. Consider the integral where C is the boundary of the desert; its value is (ζ), i.e., a lion in the cage (3).
9. THE WIENER TAUBERIAN METHOD. We procure a tame lion, L, of class L(-, ), whose Fourier transform nowhere vanishes, and release it in the desert. L0 then converges to our cage. By Wiener's General Tauberian Theorem(4), any other lion, L (say), will then converge to the same cage. Alternatively, we can approximate arbitrarily closely to L by translating L about the desert(5).
Methods from theoretical physics
10. THE DIRAC METHOD. We observe that wild lions are, ipso facto, not observable in the Sahara Desert. Consequently, if there are any lions in the Sahara, they are tame. The capture of a tame lion may be left as an exercise for the reader.
11. THE SCHRÖDINGER METHOD. At any given moment there is a positive probability that there is a lion in the cage. Sit down and wait.
12. THE METHOD OF NUCLEAR PHYSICS. Place a tame lion in the cage, and apply a Majorana exchange operator(6) between it and a wild lion. As a variant, let us suppose, to fix ideas, that we require a male lion. We place a tame lioness in the cage, and apply a Heisenberg exchange operator(7) which exchanges the spins.
13. A RELATIVISTIC METHOD. We distribute about the desert lion bait containing large portions of the Companion of Sirius. When enough bait has been taken, we project a beam of light across the desert. This will bend right round the lion, who will then become so dizzy that he can be approached with impunity.
Methods from experimental physics
14. THE THERMODYNAMICAL METHOD. We construct a semi-permeable membrane, permeable to everything except lions, and sweep it across the desert.
15. THE ATOM-SPLITTING METHOD. We irradiate the desert with slow neutrons. The lion becomes radioactive, and a process of disintegration sets in. When the decay has proceeded sufficiently far, he will become incapable of showing fight.
16. THE MAGNETO-OPTICAL METHOD. We plant a large lenticular bed of catnip (Nepeta cataria), whose axis lies along the direction of the horizontal component of the earth's magnetic field, and place a cage at one of its foci. We distribute over the desert large quantities of magnetized spinach (Spinacia oleracea), which, as is well known, has a high ferric content. The spinach is eaten by the herbivorous denizens of the desert, which are in turn eaten by lions. The lions are then oriented parallel to the earth's magnetic field, and the resulting beam of lions is focussed by the catnip upon the cage.
(1) By Hilbert. See E. W. Hobson, The Theory of Functions of a Real Variable and the Theory of Fourier's Series, 1927, vol. 1, pp. 456-457.
2) H. Seifert and W. Threlfall, Lehrbuch der Topologie, 1934, pp. 2-3.
(3) N.B. By Picard's Theorem
(W. F. Osgood, Lehrbuch der Funktionentheorie, vol. 1, 1928, p.748), we can catch every lion with at most one exception.
(4) N. Wiener, l. c., p. 89.
(5) N. Wiener, The Fourier Integral and Certain of its Applications, 1933, pp. 73-74.
(6) See, for example, H. A. Bethe and R. F. Bacher, Reviews of Modern Physics, vol. 8, 1936, pp. 82-229; especially pp. 106-107.
(7) Ibid.
I am delighted to report that Columbia not only reproduced that above but also some further contributions. I have omitted the content of those that didn’t change.
How to Catch a Lion in the Sahara Desert
(1) THE METHOD OF INVERSIVE GEOMETRY
(2) THE SET THEORETIC METHOD: previously Mengentheoretisch.
(3) THE DIRAC METHOD
(4) THE THERMODYNAMIC METHOD
(5) THE KALRA METHOD: Make a list of the lion's whereabouts. Classify them into different fuzzy sets. The lion will get confused and fall into your trap.
(6) TOPOLOGICAL METHOD:
(7) THE SCHRÖDINGER METHOD
(8) THE HEISENBERG METHOD: You will disturb the lion when [if] you observe it before capturing. So keep your eyes closed.
(9) THE EINSTEIN METHOD: Run in the direction opposite to that of the lion. The relative velocity makes the lion run faster and hence he feels heavier and gets tired.
(10) THE NEWTONIAN METHOD: Let the lion catch you (let's assume you remain alive here). For every action there is an equal and opposite reaction. Therefore, you will have captured the lion.
(11) THE CARTESIAN METHOD: Take the origin as close as possible to the lion. Then perform rotation operation again and again. Initially, the lion will feel dizzy. Finally it will fall down.
(12) THE SOFTWARE METHOD: Make a linked list of all objects in the desert. Then delete the pointers on either side of the lion. (Make sure you are not AFTER the lion.)
(13) THE AUTOMATA METHOD: Use a Non-Deterministic Finite Automaton with epsilon moves from all states to the final state, and no moves from the final state. The lion will soon enter the final state and be trapped.
(14) THE TIME-COP METHOD: Use a time-machine and take the entire Sahara back a few years in time. The lion is just a cub now, and all you need is a mouse-trap.
(15) THE INTEGRO-DIFFERENTIAL METHOD: Integrate the Sahara over its entire surface. The lion is now somewhere in the result. Differentiate the result w.r.t the earth's rotation. The resulting value is zero, and the lion is no more.
(16) THE SHAKESPEARE METHOD: Hold the lion still for a moment (I don't care how you do it), and recite Shakespeare`s Hamlet to it. The lion will change from 'To be to Not-to-be'.
Continuing to search but from a different start point I found this, from gksoft, which advances what was in 1938 an unknown field.
Problem: To Catch a Lion in the Sahara Desert.
1. Mathematical Methods
2. Theoretical Physics Methods
3. Experimental Physics Methods
4. Contributions from Computer Science
1. The search method We assume that the lion is most likely to be found in the direction to the north of the point where we are standing. Therefore the REAL problem we have is that of speed, since we are only using a PC to solve the problem.
2. The parallel search method By using parallelism we will be able to search in the direction to the north much faster than earlier.
3. The Monte-Carlo method We pick a random number indexing the space we search. By excluding neighbouring points in the search, we can drastically reduce the number of points we need to consider. The lion will according to probability appear sooner or later.
4. The practical approach We see a rabbit very close to us. Since it is already dead, it is particularly easy to catch. We therefore catch it and call it a lion.
5. The common language approach If only everyone used ADA/Common Lisp/Prolog, this problem would be trivial to solve.
6. The standard approach We know what a Lion is from ISO 4711/X.123. Since CCITT have specified a Lion to be a particular option of a cat we will have to wait for a harmonized standard to appear. $20,000,000 have been funded for initial investigations into this standard development.
7. Linear search Stand in the top left hand corner of the Sahara Desert. Take one step east. Repeat until you have found the lion, or you reach the right hand edge. If you reach the right hand edge, take one step southwards, and proceed towards the left hand edge. When you finally reach the lion, put it the cage. If the lion should happen to eat you before you manage to get it in the cage, press the reset button, and try again.
8. The Dijkstra approach The way the problem reached me was: catch a wild lion in the Sahara Desert. Another way of stating the problem is:
Axiom 1: Sahara elem deserts
Axiom 2: Lion elem Sahara
Axiom 3: NOT(Lion elem cage)
We observe the following invariant:
P1: C(L) v not(C(L))
where C(L) means: the value of "L" is in the cage. Establishing C initially is trivially accomplished with the statement
;cage := {}
Note 0: This is easily implemented by opening the door to the cage and shaking out any lions that happen to be there initially. (End of note 0.)
The obvious program structure is then:
;cage := {}
;do NOT (C(L)) ->
;"approach lion under invariance of P1"
;if P(L) ->
;"insert lion in cage”
[] not P(L) ->
;skip
;fi
;od
where P(L) means: the value of L is within arm's reach.
Note 1: Axiom 2 ensures that the loop terminates. (End of note 1.)
Exercise 0: Refine the step "Approach lion under invariance of P1". (End of exercise 0.)
Note 2: The program is robust in the sense that it will lead to abortion if the value of L is "liones". (End of note 2.)
Remark 0: This may be a new sense of the word "robust" for you. (End of remark 0.)
Note 3: From observation we can see that the above program leads to the desired goal. It goes without saying that we therefore do not have to run it. (End of note 3.)
(End of approach.)
Komplexify, which I did not find last, did much the same as gksoft and added some entirely new ideas, where 1-11 were from the original work. 12-18 came from Morhpy who I quote here and then (13 more ideas and I quote from Komplexify in brown, having fixed minor spelling or typing errors throughout.
Otto Morphy, D.Hp.
(Doctor of Hypocrisy)
It is now 30 years since the appearance of H. Petard's classic treatise [2] on the mathematical theory of big game hunting. These years have seen a remarkable development of practical mathematical techniques. It is, of course, generally known that it was Petard's famous letter to the president in 1941 that led to the establishment of the Martini Project, the legendary crash program to develop new and more efficient methods for search and destroy operations against the axis lions. The Infernal Bureaucratic Federation (IBF) has recently declassified certain portions of the formerly top secret Martini Project work. Thus we are now able to reveal to the world, for the first time, these important new applications of modern mathematics to the theory and practice of lion hunting. As has become standard practice in the discipline [2] we shall restrict our attention to the case of lions residing in the Sahara Desert [3]. As noted by Petard, most methods apply, more generally, to other big game. However, method (3) below appears to be restricted to the genus Felis. Clearly, more research on this important matter is called for.
1. Surgical method. A lion may be regarded as an orientable 3-manifold with a nonempty boundary. It is known [4] that by means of a sequence of surgical operations (known as "spherical modification" in medical parlance) the lion can be rendered contractible. He may then be signed to a contract with Barnum and Bailey.
2. Logical method. A lion is a continuum. According to Cohen's theorem[5] he is undecidable (especially when he must make choices). Let two men approach him simultaneously. The lion, unable to decide upon which man to attack, is then easily captured.
3. Functorial method. A lion is not dangerous unless he is somewhat gory. Thus, the lion is a category. If he is a small category then he is a kittygory [6] and certainly not to be feared. Thus we may assume, without loss of generality, that he is a proper class. But then he is not a member of the universe and is clearly not of any concern to us.
4. Method of differential topology. The lion is a 3-manifold embedded in euclidean 3-space. This implies that he is a handlebody [7]. However, a lion which can be handled is tame and will enter the cage upon request.
5. Sheaf theoretic method. The lion is a cross-section [8] of the sheaf of germs of lions [9] on the Sahara Desert. Merely alter the topology of the Sahara, making it discrete. The stalks of the sheaf will then fall apart releasing the germs which attack the lion and kill it.
6. Method of transformation groups. Regard the lion as a surface. Represent each point of the lion as a coset of the group of homeomorphisms of the lion modulo the isotropy group of the nose (considered as a point) [10]. This represents the lion as a homogeneous space. That is, this representation homogenizes the lion. A homogenized lion is in no shape to put up a fight [11].
7. Postnikov method. A male lion is quite hairy [12] and may be regarded as being made up of fibers. Thus we may regard the lion as a fiber space. We may then construct a Postnikov decomposition [13] of the lion. This being done, the lion, being decomposed, is dead and in bad need of burial.
8. Steenrod algebra method. Consider the mod p cohomology ring of the lion. We may regard this as a module over the mod p Steenrod algebra. Doing this requires the use of the table of Steenrod cohomology operations [14]. Every element must be killed by some of these operations. Thus the lion will die on the operating table.
9. Homotopy method. The lion has the homotopy type of a one-dimensional complex and hence he is a K(pi,1) space. If pi is non-commutative, then the lion is not a member of the international communist conspiracy [15] and hence he must be friendly. If pi is commutative, then the lion has the homotopy type of the space of loops on a K(pi,2) space [13]. We hire a stunt pilot to loop the loops, thereby hopelessly entangling the lion and rendering him helpless.
10. Covering space method. Cover the lion by his simply connected covering space. In effect this decks the lion [16]. Grab him while he is down.
11. Game theoretic method. A lion is big game. Thus, a fortiori, he is a game. Therefore there exists an optimal strategy [17]. Follow it.
12. Group theoretic method. If there are an even number of lions in the Sahara Desert we add a tame lion. Thus, we may assume that the group of Sahara lions is of odd order. This renders the work capable of a solution according to the work of Thompson and Feit [18].
We conclude with one significant non-mathematical method.
13. Biological method. Obtain a number of planarians (flat worms) and subject them to repeated recorded statements saying: "You are a planarian." The worms should shortly learn this fact since they must have some suspicions to this effect to start with. Now feed the worms to the lion in question. The knowledge of the planarians is then transferred to the lion [19]. The lion, now thinking that he is a planarian, will proceed to subdivide. This process, while natural for the planarian, is disastrous for the lion.
Ed. Note: Prof. Morphy is the namesake of his renowned aunt, the author of the famous series of epigrams now popularly known as Aunti Otto Morphisms, or euphemistically as epimorphisms.
Footprints
[1] This report was supported by grant #007 from Project Leo of the War on Puberty.
[2] H. Petard. A contribution to the mathematical theory of big game hunting, Amer. Math. Monthly 45 (1938) p446-447.
[3] This restriction of the habitat does not affect the generality of the results because of Brower's theorem on the invariance of domain.
[4] Kervaire and Milnor, Groups of homotopy spheres, I, ann. of Math., (1963).
[5] P. J. Cohen, The independence of the continuum hypothesis, Proc. N.A.S. (63-64).
[6] P. Freyd, Abelian Categories, Harper and Row, New York, 1964.
[7] S. Smale, A survey of some recent developments in differential topology, Bull. A.M.S. (1963).
[8] It has been experimentally verified that lions are cross.
[9] G. Bredon, Sheaf Theory, McGraw-Hill, new York, 1967.
[10] Montgomery and Zippin, Topological Information Groups, Interscience, 1955.
[11] E. Bordern, Characteristic classes of bovine spaces, Peripherblatt fur Math., (1966BC).
[12] Eddy Courant, Sinking of the Mane, Pantz Press, 1898.
[13] E. spanier, Algebraic Topology, McGraw-Hill, New York, 1966.
[14] Steenrod and Epstein, Cohomology Operations, Princeton, 1962.
[15] Logistics of the Attorney General's list, Band Corp. (1776).
[16] Admiral, T.V., (USN Ret.), How to deck a swab, ONR tech. rep. (classified).
[17] von Neumann and Morgenstern, Theory of Games..., Princeton, 1947.
[18] Feit and Thompson, Solvability of groups of odd order, Pac. J. M. (1963).
[19] J. V. McConnell, ed., The Worm Re-Turns, Prentice-Hall, Englewood Cliffs, N.J., 1963.
[20] This method must be carried out with extreme caution, for if the lion is large enough to approach critical mass, the fissioning of the lion may produce a violent reaction.
The Komplexify site improved some of these by better writing, but I erased most of those so you can find them yourself from the links. Again, typos fixed, which means, if nothing else, that I have read them.
Recent, hitherto unpublished, work has revealed a range of new methods:
19. The field-theory method. Irrigate the desert and plant grass so that it becomes a field. A zero lion is trivial to capture, so we may assume the lion L is nonzero. The element 1 may be located just to the right of 0 in the prime subfield. Prize it apart into LL-1 and discard L-1. (Remark: the Greeks used the convention that the product of two lions is a rectangle, not a lion; the product of 3 lions is a solid, and so on. It follows that every lion is transcendental. Modern mathematics permits algebraic lions.)
20. The kittygory method. Form the category whose objects are the lions in the desert, with trivial morphism. This is a small category (even if lions are big cats) and so can be embedded in a concrete category [11]. There is a forgetful functor from this to the category of sets: this sets the concrete and traps the embedded lions.
21. Backward induction. We prove by backward induction the statement L(n): "It is possible to capture n lions." This is true for sufficiently large n since lions will be packed like sardines and have no room to escape. But trivially L(n+1) implies L(n), since having captured n+1 lions, we can release one. Hence L(1) is true.
22. Another topological method. Give the desert the leonine topology, in which a subset is closed if it is the whole desert, or contains no lions. The set of lions is now dense. Put an open cage in the desert. By density, it contains a lion. Shut it quickly!
23. The Moore-Smith method. Like (5) above, but this applies to non-separable deserts: the lion is caught not by a sequence, but by a net.
24. For those who insist on sequences. The real lion is non-compact and so contains non-convergent subsequences. To overcome this let Omega be the first uncountable ordinal and insert a copy of the given lion between A and A+1 for all ordinals A less than Omega. You now have a long lion in which all sequences converge [12]. Proceed as in (5).
25. The group ring method. Let G be the free group on the set L of lions, and let ZG be its group ring. The lions now belong to a ring, so are circus lions, and hence tame.
26. The Bourbaki method. The capture of a lion in the desert is a special case of a far more general problem. Formulate this problem and find necessary and sufficient conditions for its solution. The capture of a lion is now a trivial corollary of the general theory, which on no account should be written down explicitly.
27. The Hasse-Minkowski method. Consider the lion-catching problem modulo p for all primes p. There being only finitely many possibilities, this can be solved. Hence, the original problem can be solved [13].
28. The PL method. The lion is a 3-manifold with nonempty boundary. Triangulate it to get a PL manifold. This can be collared [14], which is what we wish to achieve.
29. The singularity method. Consider a lion in the plane. If it is a regular lion its regular habits render it easy to catch (e.g. dig a pit). Without loss of generality, it is a singular lion. Stable singularities are dense, so without loss of generality the lion is stable. The singularity is not a self-intersection (since a self-intersecting lion is absurd) so it must be a cusp. Complexify and intersect with a sphere to get a trefoil knot. As in (7) the problem becomes trivial.
30. The measure-theoretic method. Assume for a contradiction that no lion can be captured. Since capturable lions are imaginary, all lions are real. On any real lion there exists a nontrivial invariant measure m, namely Harr or Lebesgue measure. Then the product m x m is a Baire measure on L x L by [15]. Since a product of lions cannot be a bear, the Baire measure on L x L is zero. Hence, m=0, a contradiction. Thus, all lions may be captured.
31. The method of parallels. Select a point in the desert and introduce a tame lion not passing through that point. There are three cases. (i) The geometry is Euclidean. There is then a unique parallel lion passing through the selected point. Grab it as it passes. (ii) The geometry is hyperbolic. The same method will now catch infinitely many lions. (iii) The geometry is elliptic. There are no parallel lions, so every lion meets every other lion. Follow the tame lion and catch all the lions it meets: in this way, every lion in the desert will be captured.
32. The Thom-Zeeman method. A lion loose in the desert is an obvious catastrophe [16]. It has three dimensions of control (2 for position, 1 for time) and one dimension of behaviour (being parametrized by a lion). Hence by Thom's Classification Theorem it is a swallowtail. A lion that has swallowed its tail is in no state to avoid capture.
33. The Australian method. Lions are very varied creatures, so there is a variety of lions in the desert. This variety contains free lions [17], which satisfy no nontrivial identities. Select a lion and register it as "Fred Lion" at the local register Office: now it has a nontrivial identity, and hence cannot be free. If it is not free it must be captive. (If "Fred Lion" is thought to be a trivial identity, call it "Albert Einstein.")
Bibliogoraphy
[1] H. Petard. A contribution to the mathematical theory of big game hunting, Amer. Math. Monthly 45 (1938) 446-7.
[2] E. W. Hobson, The theory of functions of a real variable and the theory of Fourier's series, 1927.
[3] H. Seifert and W. Threlfall, Lehrbuch der Topologie, 1934.
[4] N. Wiener, The Fourier integral and certain of its applications, 1933.
[5] O. Morphy, Some modern mathematical methods in the theory of big game hunting, Amer. Math. Monthly 75 (1968) 185-7.
[6] M. Kervaire and J. Milnor, Groups of homotopy spheres I, Ann. of Math. 1963.
[7] This footnote has been censored by the authorities.
[8] It has been verified experimentally that lions are cross.
[9] E. Spanier, Algebraic Topology, McGraw-Hill 1966.
[10] W. Feit and J. G. Thompson, Solvability of groups of odd order, Pac. J. Math. 1963.
[11] P. Freyd, Abelian Categories.
[12] J. L. Kelley, General Topology.
[13] J. Milnor and D. Husemoller, Symmetric Bilinear Forms, 1973.
[14] C. P. Rourke and B. L. Sanderson, Itroduction to Piecewise Linear Topology, 1973.
[15] S. K. Berberian, Topological Groups.
[16] R. Thom, Stabilite Structurelle et Morphogenese, 1972.
[17] Hanna Neumann, Varieties of Groups, 1972.
I noticed just this morning that the lion has long been missing from the Sahara. Clearly at least one of these methods is successful.
DJS 20170711