It’s very sad, but Dad has gone gaga. A man whose primary asset was his mind has lost the very thing he most valued. His current condition is such that he is in a care home and communication is very limited. Output from him is little more than wo-da-wo-da, usually 10-16 syllables of this, with just the rare comprehensible word. Reaction to input shows not a lot more. He is mobile, he can maintain himself with a little care support, he is largely amenable. Descriptions of old age as a return to a child-like existence are accurate enough in the sense that he is dependent in much the same as an infant just into walking, only with none of the excitement. I am unsure that he recognises anyone, uncertain whether he hears anything and this causes me to wonder about thinking, communication and our perception of its need.
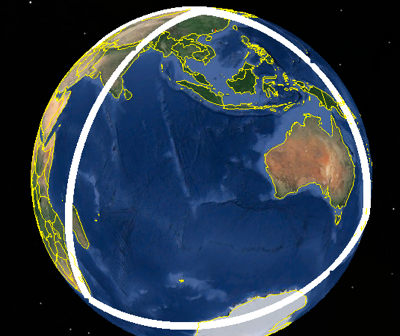
Father was a very able thinker. Past tense applied, but more on that later. He was a mathematician who worked in computing. Let me characterise what that means: In the time since he retired he spent many months thinking about the geometry of triangles drawn on a spherical surface, which he collapsed to ‘spherical triangles’. Before you switch off completely, please think about this just a little. If the sphere is large compared to the triangle, say the triangle is on your floor and the sphere is Earth, then there is very little difference between your triangle and a 2-d, flat surface. The angles add up to 180º. However, if the triangle has vertices as far apart as say Britain, SE Canada, NE Brazil—let’s say Bristol, New Brunswick and Recife—then you clearly have more than 180º [80+95+45=220]. I suggest you might have fun with Google Earth at this point. If you swap Bristol for Beijing, you’re close to 300º, 65+145+85=295. Swap Recife for CapeTown and [112+120+105=337] all three angles are bigger than a right angle; connect Cape Town, Beijing and Auckland, enveloping the Pacific and Australia, and the triangle barely stays on the face of the globe (as) you can see at the top. Choose Cape Horn, the Cape of Good Hope and a point on the Kamchatcka peninsula about 2/3 from top to bottom and the three points lie on a circle, suggesting 540º [or 3π] in the ‘triangle’. Is this the limit? Well, if you go play with drawing paths on Google Earth like I did, yes. But I suggest that you can draw the lines yourself to wrap around even more than this and challenge you to find the upper limit for what is now three arcs of great circles joining points on a spherical surface. Example; take the triangle seen nearby and move the bottom left point even more to the left and around the back until it reaches Perth, western Australia. Two angles became larger; repeat this idea and maybe the total angle exceeds 3π. Or maybe not. Father found this ‘interesting’. I put that in quotes because he must have devoted several weeks’ worth of time to the idea. For example, three months I know about were spent of the sub-set of triangles whose total angle was 2π. He did this sort of thing often.
The sort of black & white distinction that mathematical thinking demands (discuss, please), that same thing that makes middle range school-kids actually ‘like maths’, demands a clarity of thought that few of us apply to other walks of life. Some would say nothing in maths is applicable to real life.
My younger brother was describing an issue with form filling that might reflect this sort of (maybe weird to you) thinking: Let’s say you’re asked about your ethnicity; you might choose not to reply, reported as ‘ethnicity not stated’ and box to that effect ticked; the case where the question was not put, perhaps because because someone forgot or no opportunity arose, is then a null response. Do you think these are the same? He says not, and I agree. You may say you don’t care. But then what happens if the null response numbers are large compared to the whole? What happens if you decide that all the ‘unstated’ cases require a later guess (”Oh, it’s obvious they’re all ‘White British’”). Is that the same as doing this to the null response cases? I say not. If you agree, that means that we have two different sorts of zero. In set theory, this is the difference between {0} and {}; one set containing the zero and the other the properly empty set. Such descriptions may leave you saying “Why would I care?” or likely more extreme disinterest. Well, some of us do care that there is a difference. Stick with me a moment longer...
One unlikely consequence of such thinking occurs if the same sort of fine distinction is applied internally. This I might describe as internal honesty. Father was very good at this. ‘Good’ is not what most people would call this, because the result would be an honesty you didn’t want to hear. Think “Does this <clothing> suit me?” “Does my bum look big in this?” Question far better not put, since he would tell the truth as he saw it. Your feelings about that response were judged irrelevant, not providing any condition to affect the truth of that response, not even in changing the response to, say, ”Do you really want an opinion?”. Which, from most mouths, would be taken to mean as something negative, where, on the very rare occasions he would say such, he would mean more nearly, “Do you really want to hear from me when you know the sort of thing I will say? I’ll give you an opinion as asked”. All of which sometimes made him difficult to talk with, but only because the second party, the ‘you’ talking with him, had not taken into account who it was they were talking with.
In turn, this intellectual honesty had its own consequences. For a start, every subject rapidly became academic in the sense that often you’d move rapidly from the specific to the general. So if you asked a question that belonged in what we might call a no-go area like clothes, for the reasons above, you’d soon find yourself considering what clothes are for in general, how this related to the occasion in question, what therefore the requirements were for clothing and in consequence what you were going to do about it. Or, indeed, after any such single occurrence, not needing to have the conversation at all because you could do it equally well on your own. Which probably explains why so many find the family downright weird.
Now I’m not saying in any sense that this resulted in him being ‘right’ about everything. Or indeed about anything except certain bits of mathematical application. This sort of thinking does not bring social success (definitely); it is not valued by employers; it doesn’t bring relevant but missing information into view, though it might point to a lack. On the other hand it does indirectly point to a set of questions we might ask of the rest of the world: How much are you lying to yourself? How much lying do you do? How do you feel about this? Do you even notice the gaps between what you say, what you mean, what you think and what you tell yourself you think? To what extent do you tell people what you think they want to hear? If the world revolves around communication, is this behaviour in any sense ‘good’?
The state of Father is not a good place to be. I wrote above that he was an able thinker: The lack of response to external stimuli tells us that input is not producing output. That does not tell us that the brain is not functioning, it only says communication fails, and even then, only for certain in one direction. For all I know (pitifully little), he is still exploring the geometry of spherical triangles and if so then I’m fairly sure he is happy, inside. He does throw tantrums which all assume to be born of frustration at failing to make output comprehensible. However, his legacy is that some of us know how to think as I described at length above and a few of us cannot help ourselves for we do it automatically. In terms of social acceptability, this makes us difficult. What then is the price of behaving sociably? Picking a route that balances internal honesty with socially acceptable responses is difficult for, too often, they are not just in imbalance but directly conflicting. Perhaps this is why so many people don’t answer the question actually posed but instead respond to the question they think is meant? Is this a recipe for good communication when everyone functions on guesswork? Does that in any way explain why the modern generation seems to use such empty forms of communication? Are we reverting to the caveman grunt?
DJS 20151208
Exercise:
0. Explain what you mean by ‘triangle' when drawn on the surface of a sphere.
- On a unit sphere (radius of length one unit), a triangle has total angle nπ radians. Assuming natural n, what are the possible values for n?
- So as to work in units of π, consider a sphere of radius π. What is the longest perimeter of a triangle whose total angle is nπ?
- What level of error (lack of precision) do you find acceptable? Consider the error in angle of an equilateral triangle drawn on spherical surface radius π. What is the perimeter required for angular error to reach p%? Conversely, if two angles are defined as π/3, how does the third angle change with increasing (roughly equal) side length λ? If the third side has length λ+∂, how does the relative error ∂/λ vary and when do you consider this significant? How does this affect your opinion of treating maps as ‘flat’? What corrections might be appropriate over a map of Britain? What about Australia? (similar responses would apply to Canada, China, India and the US).
Any proferred answers will result in discussion.
Father eventually died 20 April 2016. See Magnetism.
Looking at various other things, I discovered a number of papers by Father (who was always telling me how he was being told off by others for not publishing). He never talked about the published work, though ~~i did persuade him once to talk about his PhD thesis, in which he tried to predict the bond angle in a water molecule (unknown then, but known to be not 180º)
1951-53 with Prof Stanley Rushbrooke, seminal work on the direct correlation function in statistical mechanics (triggering a Nobel prize twenty years later for Ken Wilson). Quoted widely, I discovered.
1953 On the Theory of Fluids. 1955 Ising Problem and Mayer’s cluster sums.
1956 with HC Bolton (Uncle Bert, a godfather of mine), a treatment of eigenvalue problems and Schrödinger equations.
1962 The number of trees with nodes of alternate parity (Cambridge Philospohical Soc)
1964 Compact representation of a rooted tree
1967 Linear graphs and trees (in Machine Intelligence)
1968 placing trees in lexicographical order (in Machine Intelligence)
Monday, 7 December 2015
