I am thoroughly tired of the apparently endless succession of question on Quora asking whether <time> for <distance> at <age> is ‘good’. Is a seven minute mile okay if I’m 18? Is an hour for 10km ‘good’? It depends on so many things including whether ‘good’ applies, or what ‘good’ might mean. A 7 minute mile might well be pretty good if you’re over 60 or under 12, if your BMI is over 30 or if you’ve recently been through major surgery. An hour for a 10km is not quite so good, but again, ‘good’ is hugely subjective and needs to be in context.
However, one can remove the age element from the question. If you have not come across this, welcome to the concept of age-grading. I’m going to attempt to fix all those questions I find so irritating, because they really all deserve the same answer: “go look at age-grading". But they don’t or won’t bother to ask a better question so as to have a better answer.
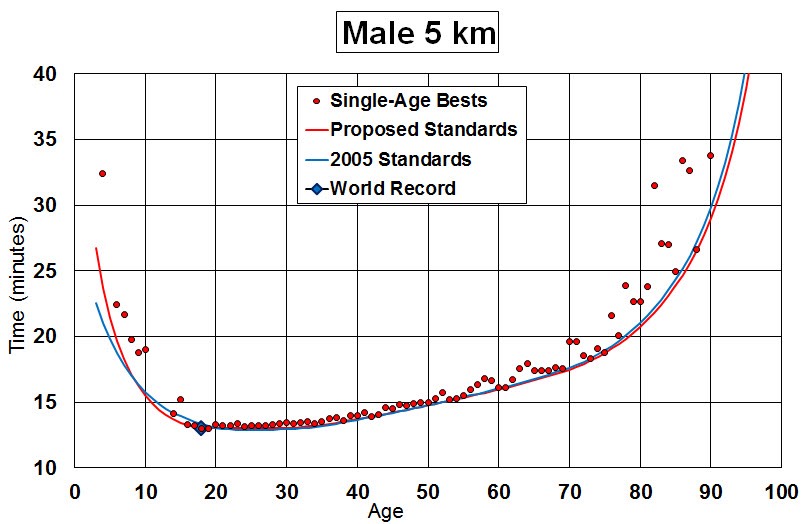
At heart, the tables are created by there being lots of data of results from athletics and running events at which age is also recorded. Indeed, once the Masters tables¹ began, so the addition of age to a record became standard. Having established what a world record is for an age, interpolating as appropriate² and applying some smoothing, your ‘age-grading’ is expressed as a percentage of the world record speed for your age. Since this is smoothed, it is still possible for an exceptional 100+% event to occur - and it has done. Enough of these exceptions causes the tables to be revised. For example, the single age records for ‘long’ distance (5, 10, 21.1 and 42.2 km) include 65/322, a nice round 20% of them, over the 100% mark, suggesting that the tables should be revised. As [3] says of the graph I copied form there and shoved above, There are very small differences between the 2005 Standards and the Proposed Standards. The very young youth standards have been softened because some earlier times for young runners have not survived scrutiny. On the other hand, upper teen year standards have been toughened because of fast times run by young Africans. This carries through for all distances… There is a drift away from the target curve above 70, but some exceptional people show that the curve might well be right, so I see this as the running population over 70 being really rather small. The ladies have been doing similarly well - see [3] for yourself, please.
A too-swift glance at the ends of the curve says that this is not a best fit; that is the wrong idea. What is sought is the envelope, the lower bound of physical performance. So those dots to the right and left that are quite a way off the line are the best that has happened (and been recorded), but quite inferior to a relatively adjacent run. That 5km time at 88, for example (and no doubt he will be having a good go at 89, too). That relatively poor time at 15, when someone a year younger is around a minute faster. There’s a Ukrainian lady whose times are so good they form an excluded outlier (they change the envelope significantly). The same has been done with African runners, where the age is in doubt, and Chinese runners, where the authenticity is in doubt.
The smoothing itself is pretty straightforward once that last point is understood. what is delightfully consistent is the table of ‘factors’ the age adjustment for a particular distance/ As [3] says of this, We found that we can use the same factors from 1500 m (we did not work on distances less than 1500 m) through 10,000 m for males and from 1500 m through 10 miles for the females. Above those distances different factors are used for each distance. Which may tell you that there are some exceptional performances skewing the figures, or that there are some likely to appear.
I’m going to address the male 5km figures, but hope to do this in a way that you can see how to work out what interests you - or simply bother to go to [2] and find the answer you want, perhaps by giving the calculator several items of work.
Here is a chart I made showing the age-grading factors for men (blue) and women (orange, not pink) for 5km not-track, so called road. Yes, it hits a ceiling around 18-30, when you times have no age-adjustment and then it decays in a regular, even surprisingly linear manner to late age. I see the men as decaying from 35 to 70 as remarkably straight (linear) at 0.672% decay per year while the women’s figures run ten years later, from 45 to 80 at 0.971% decay per year (I’ll accept some dispute over that last digit)³. I observed a 1% decay in my own performance once I passed 50; discovering that there is a more precise figure that is so close is a help.
The modelling (and I may produce some maths exercise to study this) is separated into Youth (before the age-factor is unity, gradient positive) and masters (past-it, gradient negative). The flat part is joined to the linear part by a parabola, followed by another parabola for the very much older runner. If I pursue this thread, it will be in the maths section with a link here.
So, what is a ‘good’ time? There are many ways to answer this, but I’ll pick two, the personal and the regional.
What is a good time for you? That depends entirely on you having some idea of any history of times and distances. If you are moving from no exercise to some exercise, well done and please feel encouraged to continue. Keeping track of times and distances (possible also weather, health, route, time of day and other stuff you think relevant) will only serve to encourage - because generally the figures will improve. Age-grading is not relevant to you unless you were a runner / athlete many years ago and want to compare then and now, especially having had a lot of time off, like decades.
Is the time you’re doing 'good' in a more absolute sense? The % of record pace that the age-grading tables produce is a good way of measuring, because it separates the distance/time information from the performance. If you’re doing several distances, the tables allow you to discover if you’re actually genuinely better at some event than another. Imagine you’re at 60% on 100m but 65% at 800m and 70% at 5000m. Is that not a hint at what you’re good at? If you dramatically prefer the shorter distances, it tells you how to address training and sets you a standrad to aim for - clearly, to me, if 70% is happening at one event, that is the target for other events, since the body has shown itself capable of that performace level.
The ‘absolute’ nature of age-grading answers questions like “Is this good for a 10-yr old?”. [4] shows the ESAA standards (English Schools Athletics Association) and provides three times / distances, labelled CS, ES and NS, the standards at County, Entry and National, where County means a good performance at County level, Entry means the level for selection to represent the County, and National is that bit better still, with some attached award and perhaps drawing some external interest. The 5000m is not on this list, but the 1500m and 3000m are. I added in the Schools Secondary award scheme which seems to be a pretty general or even crude affair, so input the times for the three ages to be found in such schools. I put all the age-graded % in blue. So National Standard is very good, at 85-90%, County Standard is also very good, at 78-84%, and the school standards are perhaps something to aim at, so that if you were to reach the gap between Silver and CS, you’re moving from ‘able to run’ to ‘a runner’. Or as someone I met after a parkrun had it yesterday, everyone over 70% was a ‘real runner’. Source: me, though the times come from the listed sources.
What is important here is the same two-fold measurement: (i) you’re comparing <yourself now> to <yourself at some other age> and (ii) you see where you fit in comparison to the record. This is not where you fit in the population, though. I ran at around 78% in races and finished in the 96th percentile (the top 4%) pretty consistently. That tells you as much about who turns up to races as it does about what 78% means in terms of finishing position. These days, 78% is a very good day for me and, being ancient, equates to 62% 30 years earlier, more like the top fifth in a wide-distribution run like a parkrun, but well into the bottom half, below the 40th percentiile, in a club race. See, it is who turns up. At a parkrun, a 78% performance might put me in the top three on age-grading - again, it depends who turns up. But 78% now defines ‘a good day’. It also shows why I was never quite at County Standard on the track; even on what I would call a good day, I was still at the bottom edge of County Standard.
How else might you categorise 'good' in terms of running ability? What about the number of people that can run at that pace, or where your pace fits into the distribution? My figure above of 78% age-grading leaving me in the the top 4% doesn't indicate much more than the nature of the spread of the distribution. It is not at all clear what proportion of the population is able to run at or better than a given speed. The distribution curve is missing. At best, we can make some sort of a guess, but the population is that which runs, quite a distinct sub-population from the general people of a nation.
Trying to articulate that further, here’s a graph showing age-grading against time for a parkrun. I’ve added a logarithmic trend line because that fitted the data best. The dot at (2347, 64.38%) that looks like an outlier is a very special gent of 86. DJS is at (1297, 77.56%). The very good people didn’t turn up this week. I suggest you study the graph as showing the trend line and a secondary distribution at right angles to that, but you must also recognise that this is a very select group of those willing to run 5km on a Saturday morning in company.
Thinking of school age performances, over 65% on age-grading is competitive and at 75% you might win at your school and lose against other schools—it all depends who turns up. At better than 75% you’re in demand to be in a school team. Age is not relevant here, because you’re looking at age-grading. Embarrassing though it is, to match my 78% at 5000m, you’d be aged just over 8½ and in Year 4 in Britain. No wonder than that I find myself racing the 10-14 year olds at parkrun. Looking for support for this opinion, I found [6], which is altogether more flattering: over 60% Local Class, over 70% Regional, over 80% National, over 90% World class. That puts me at the good end of ‘Regional' and still naturally 4th in the 60+ at our local parkrun if the usual guys turn up. Like I said, seriously competitive. I’d add 5% to each of these, but I'll accept I might be biased. [6] addresses the question if you are a “Regional” class athlete, how often might you win your age group in a 5K road race?. At last, someone approaching what I think ‘we’ want to know–and couched in language I like:
As an example, consider “Joe”, a 32 year old male who can run a 5K in 21:33. The WMA 2015 standard for a 5 km road race is 13:05. With a time of 21:33, Joe will perform at 60.7% of the standard, and hence is just above the threshold for a “local class” athlete. We will also note that a time of 21:33 also corresponds to the 87.29th percentile among 32 year old males.
Among all male and female 5K finishers of all ages, 4.9% are males between 30 and 34[ref]. Suppose “Joe” decides to participate in a very small race expected to have just 40 total runners in addition to himself. He would then expect to compete against an average of 40 x 4.9% = 1.96 other runners in the M30-34 age group. If the expected 40 runners are a representative sample of all runners, then the actual number of runners in the M30-34 age group will follow a Poisson distribution with mean 1.96.
Using Poisson distribution with a mean of 1.96 suggests there is a reasonable probability (0.141) that no other competitor shows up for Joe’s age group and he will then have a 100% chance of winning his age group. There is a probability of 0.276 that exactly one other competitor shows up in the M30-34 age group. Since Joe is calculated to be at the 87.29th percentile among his peers, he will have a 0.8729 probability of defeating this competitor. Thus the probability that exactly one other age group competitor shows up and that Joe beats him is 0.276 x 0.8729 = 0.241. The Poisson probability that Joe has exactly 2 competitors is 0.271 and the probability that he beats both is 0.8729 x 0.8729 = 0.7620. Thus, the combined probability that exactly 2 competitors show up and that Joe beats them both is 0.271 x 0.7620 = 0.206.It is possible to make similar calculations for every possible number of competitors for Joe in the M30-34 age group, i.e. for 0,1,2,3,4,5,6 . . . etc. When we add up the probability that Joe wins his age group across all possible numbers of competitors, we can calculate that Joe’s overall probability of winning is 0.141+0.241+0.206+0.118+0.050+0.017+0.005+. . . = 0.779. Thus, a male between 30 and 34 who competes at 60.7% of the WMA standard will have approximately 0.779 chance of winning his 5-yr age group in a race expected to have a total of only 40 other participants. Since Joe, competing at 60.7% of the WMA standard, will usually win his age group in these very small races, we can correctly state that a 60.7% age-grade is significantly superior to the typical age-group winner in a race with just 40 participants.Now suppose that Joe participates in another race expected to have 110 total participants in addition to himself. In this case, if we go thru the above calculations for the larger race, we find that Joe will have “only” a 0.501 probability of winning the M30-34 age group. Thus, half of the time Joe will win his age group and half the time he will not. Consequently, we can conclude that, among males 30-34, a 60.7% age-grade is equivalent to the median or typical age-group winner in races having a total of 110 participants.
One of the things I take from the above is that the writer has found a population distribution: We will also note that a time of 21:33 also corresponds to the 87.29th percentile among 32 year old males. I failed to find such a thing, or maybe I failed to be satisfied that the things I found were indeed what I was looking for. But read on.
The Median WMA AG graph, also from [6], is perhaps self-explanatory. The female winners are consistently given an age-grading 4% below the men, so for direct comparison add 4% to the woman’s AG [if she’s at 66%, she’s performing equivalent to a man at 70%]. All of this assumes that the people that turn up to races are themselves a representative sample of the running population and by implication that assumes that everyone turns up to the same number of races. This is clearly not true, though I suppose it is possible that the behaviour of the population as a whole equates to that. My observation is that people having a ‘good’ year will go to more races, in some sense chasing glory. The very good and very confident will carefully choose their races, adding to the likelihood of attendance at a large race; this confuses quantity with quality, but is typical of the sort of assumptions one makes in mathematical modelling and statistics.
Better still, source [7] provides the distribution of percentiles for males and females in each ten-year group. I’ve attempted to produce graphs from one of these tables so you can see the general shape of the distribution. The y-axis is time in 3 minute intervals and the x-axis is percentile of the population, so 100% is the world record after age adjustment. I added a trend-line for each to help you see the sets, using a quintic because it fitted better than the alternatives. The data is from the US and I have no idea how that compares with Britain. I suggest that Britain’s figures are different, since according to this, my being consistently inside 22 minutes puts me in the last 1% and my pal Paul in the last 0.1%. That would, though, agree with my comment about who turns up and whether they represent the running population; in small numbers I don’t think they do. if the running population from 60 onwards is already reduced to only those who still can run, and if it is probable that most of these have been runners historically, then this is indeed a heavily biased population. I imagine a few newly retired decide to do something about body shape, but I’m not seeing data for them in our parkrun.
A recent-birthday 14 year-old finishing next to me (on the proverbial ‘good’ day) scores 64%. Is he a good runner? Quite possibly, since he turned up and ran. If he keeps on running he won’t stay at 64% for long, and he is already in the top 20% of 14 year olds. At my great age I’m simply very glad to be able to run at all and being at much the same (graded) standard as thirty years ago is absolutely brilliant. Of course, that has to be qualified as me running around that standard when I allow measurement to occur; there are far too many weeks when I don't permit measurement because i'm a long way below par, which we might call 'injured' but would be more accurate to cal 'damaged'. Satisfactory, "par" is 75%±3%: where a result will be below this I'll usually decline to run. In my head that is 'not ready', not yet fit (for running hard). the problem, as I see it, is that the head will overrule the body and I'll put myself into a damaged state by trying too hard to meet some entirely imagiined ability level.
There’s a wonderful man at parkrun most weeks (at least as often as myself) at the grand old age of 86 whose data I pinpointed in the text. He runs at around the 65% mark, which is around 38:30 minutes for the 5km and well inside the last half percentile of the general age population; occasionally he has a really good day and hits the low 70s. Even at his age, there are people 5 or even 6 minutes faster. Of course he is the course record holder for the over 80s and over 85s; the running population at his age is very small indeed. That also means, as is shown every week in the relatively young over 60s, that those who turn up are very competitive. If I finish in the top three of the over 60s, I had a good day; but it is perfectly possible for me to run a PB for the year and finish fifth of the past-its. It is even possible for me to run injured (foolish, but it happens) and have what I'd call a bad day and be 1st of the past-its. On an ordinary day I might be the first over-55, but just as easily I might be beaten by a quality lady runner in that age-group. As soon as you’re looking at position, it really does all depend on who turns up.
DJS 20181018
[1] http://bmaf.org.uk/age-graded-standards/
[2] http://www.howardgrubb.co.uk/athletics/wmalookup15.html download the spreadsheet of numbers with this Excel link or find it at [2]
[3] http://www.runscore.com/Alan/AgeGrade.html
[4] https://www.esaa.net/v2/2018/tf/tf18currentstands.php
[5] http://www.howardgrubb.co.uk/athletics/wmaroad15.html the road version, i.e. 1500m upwards and not on a track.
[6] http://www.bigdatarunning.com/tag/age-grade-standards/
[7] http://www.bigdatarunning.com/5k_percentiles/
¹ I want an apostrophe in there, Masters’ tables, tables belonging to the old folk what still run. They are not referenced with any apostrophe at all, so me adding one doesn’t help you. Hence I put the moan about that here, relatively out of the way.
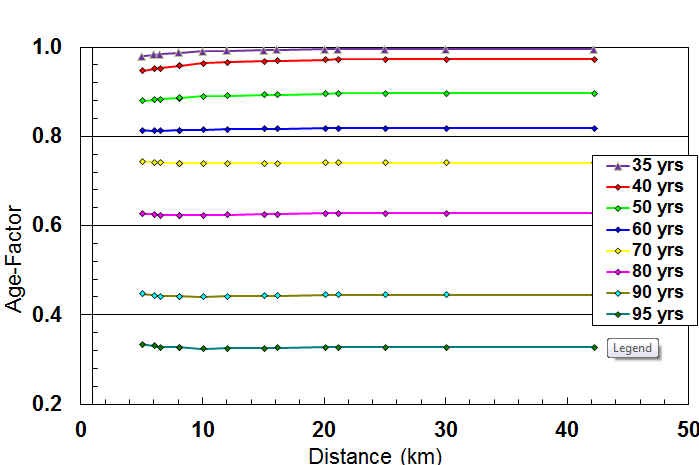
² [3]: To get the factors in the intermediate distances, the parameters were interpolated between the values obtained for those four distances. Let me make clear that the age-standards are not interpolated; it is the parameters that generate the standards which are interpolated. See [graph, right] for definitions of these parameters. To make sure there is a smooth transition as one moves to different distances, a plot of age factors was made against distance as shown below.
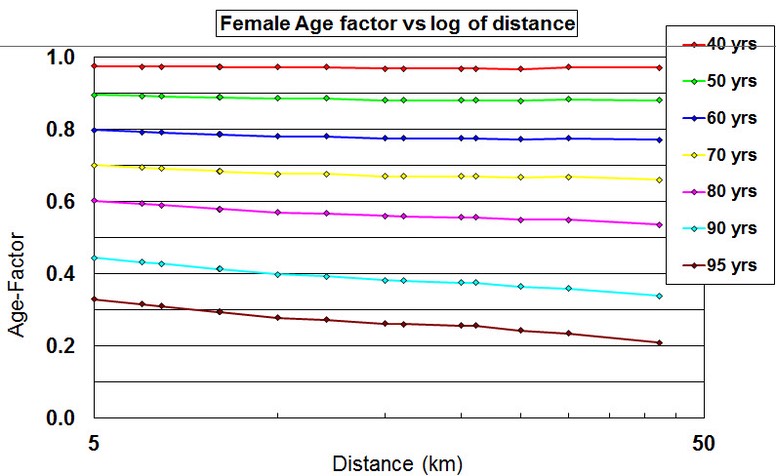
Notice, please, how constant these factors are across distances. I think it is remarkable how little decay there is from 35 to 60. The curvature seen at the shorter distances for 35-60 says that older runners are closer to the open class times than the younger runners. [3] provided a different equivalent graph for the women, which I’ve left a little smaller, which {3] comments as indicating that the female runners are closer to the open class times at the shorter distances whereas the male runners are better at the longer distance.
³ I ran regression, using LINEST in Excel, on the data for the chart to get these figures. There was very little change in the gradient of the line of best fit depending where I began the series; e.g. the women’s figure moved from 0.971 to 0.972 if I moved the start to 50, and the men were at 0.672 with starts from 46-49, with the last digit one smaller as the range to 70 grows. So the decay number given is pretty reliable.
EDITS: Whole page edited for numerous typos 20190210. Some rewriting occurred.