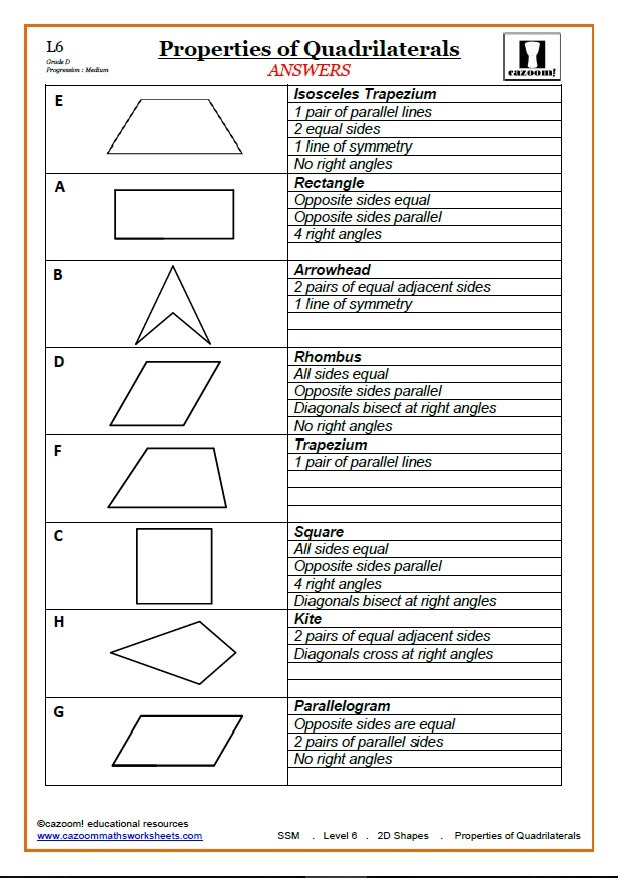
Four sided figures made of straight lines are generally known as quadrilaterals. KS3 anbd KS4 maths requires us to be able to name them and toi recognise many features, such as whjether the have parallel sides, and/or equal sides, what sorts of symmetry they have, and so on.
Wikipedia is helpful here:
These can and should be classified as follows, where * indicates that the number might increase or the value change in special cases:
Square Rectangle Rhombus Kite Parallelogram Isos Trap Scalene trap
Pairs of parallel lines 2 2 2 0 2 1 1
Equal length lines 4 2pr 2pr 2 pr 2pr 2* 0*
Right-angled corners 4 4 0 0 * 0 0 0*
Axes of symmetry 4 2 2 2 0 1 0
Rotational symmetry 4 2 2 1 2 1 1
Equal diagonals Y Y N N N Y N ‘equidiagonal'
Diagonals perpendicular Y N Y Y N N* N ‘orthodiagonal'
Diagonals bisected 2 2 2 1 2 0 0
The arrowhead is a kite of sorts, but the diagonals only meet when extended outside the shape, so it includes a reflex angle, bigger than 180º. This is an example of a concave quadrilateral, as opposed to convex.
A kite with two opposite right-angles is called a right kite.
Please note that in the US of A what the Brits call a trapezium is a trapezoid. Americans call any quadrilateral with no parallel sides a trapezium. Blame Proclus and Hutton.
We should add to this the cyclic quadrilateral, whose vertices fit on a common (circumscribed) circle. A cyclic quad with perpendicular diagonals is Brahmagupta’s trapezium. A kite is sometime called a strombus, thanks to JH Conway (who I met at college and shared abreakfast with; the creator of ‘Life’). A rhombus is often called a diamond, which is sloppy use of English. I feel the same about oblong for rectangle.
Another class of quadrilateral has an inscribed circle, so the sides are tangents to teh circle. I have not seen these studied since 1980 (possibly 1965) and I doubt they have been since geometry was replaced by modern maths (set theory, topology, etc).
There are some special cases of trapezia:
three sides could be the same length, a special isosceles trapezium. This is Gaunt’s Trapezium.
the diagonals could meet at the perpendicular a special (but otherwise assumed scalene trapezium)
the original triangle might be a right angled one before truncation; known as a right angled trapezium or
the right angle could be in the part cut off, making a special isosceles trapezium
There is a family of isosceles trapezia whose diagonals meet at right angles. Draw these by constructing the diagonals first. One of these has three equal sides. which is the special case of Gaunt’s Trapezium.
It was Tim Gaunt that poiinted out in class (about 1998) that this last triangle existed, but as a class we extended his definition to fit that larger collection with three equal sides. We could both make a case that the same label could be applied to all isosceles trapezia with perpendicular diagonals. However, since we can draw irregular quadrilateral which have mutually perpendicular diagonals, this case is rejected and as yet without a name. I can say that those I have drawn are easy to see instead as tetrahedra soilid rather than plane.
Another special case simply has two opposite sdides of the smae length; this is a Watt Quadrilateral. Gaunt’s Quadrilateral has three sides the same length. One more, from Wikipedia: A Hjelmslev quadrilateral is a quadrilateral with two right angles at opposite vertices. e.g. the right kite.
You can draw four straight lines and not form an acceptable (simple) quadrilateral (KS3 and KS4). Easily done, simply allow two sides to cross and join their ends. This would then be self-intersecting (hence also called complex) and a nice term would be butterfly or bow-tie. All will have two reflex angles. You can class these in much the same way as those enclsing a single space. Intersting is the anti-parallelogram; teh non-adjacenmt sides have equal length. I’ll let you draw that.
If you wish to ewxplore this as a topic (perhaps within IB), have a look at the secondary quadrilateral formed by joining the midpoints of sides. This is called the Varignon parallelogram. Obvious thing to go prove, there. Obvious statement here tells you what a bimedian is: the diagonals of the Varignon parallelogram are the bimedians of the original quadrilateral.
I recommend A-level students thinking of Oxbridge to look at the wikipedia entry and see if they could prove the trig dentitities offere, or any of the area formulae. This struck me as a rich field for extension questions within the A-level syllabus, therefore suitable for entry paopers and the like.
To prove (for the ambitious):
In a cyclic quadrilateral ABCD, midpoints KLMN (K is ias the midpoint of AB, L of BC and so on). Lalbel the centre of the circumscribing circle O, as usual. Construct altitudes (they’re called maltitudes) from each midppoint K,L,M,N to the opposite side.
(i) Show that these maltitudes are concurrent and call this point T, the anti-centre.
(ii) Find the centroid of the four vertices, G and show that it lies on OT
(iii) Show that G is the midpoint of OT.
If this proves too difficult, start instead from the special case where ABCD also has AC and BD perpendicular and prove that T, the anti-centre, is where AC and BD meet. Or you could call the intersection T and show this is one every maltitude.
Show would be easier than Prove, I suspect. I think I’d start this by drawing it andf then attempt using vectors for the proof, rather than the algebra of co-ordinate geometry. Back in the 1960s (year 9 especially) I would have used some geometry now long forgotten and added it to the proofs I reworked in the sixth form using the new aapproaches that A-level(s) provided. Or given it to Dad to do (and then wait at least a week).
DJS 20180410