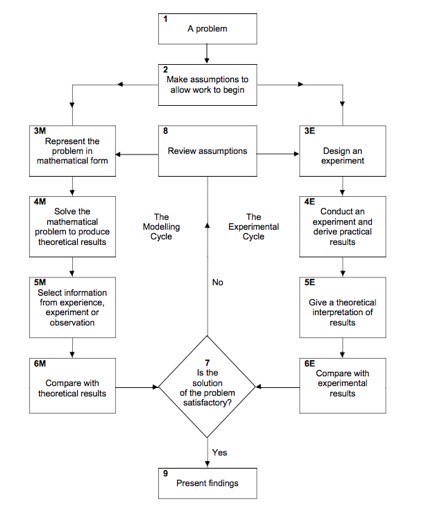
A long time ago I gave an Assembly close to Christmas pointing up the aspects of mathematical modelling that apply to the behaviour of Christmas. I cannot find that file. So here is a revisit to the topic. Originally I was passed the idea from a pal sending email; searching I found only three different versions – there are probably other files in collections of jokes, but surely this, as an idea, is made for geeks and nerds. I’d like to think of it as a challenge to mathematical modelling approaches. In this, I lean heavily upon principles expressed so well in the diagram that MEI used to use for it’s A-level maths coursework – I paraphrase: establish your assumptions; classify them by degree (of effect), explore the effects of your model; test the results to see if you like the effects of your assumptions – this includes comparing your results with ‘real-world’ data; revise your assumptions (or the expression of them) and traverse the diagram once more; repeat until any of the following occurs: nausea, boredom, satisfaction, counter-example (which usually means that the initial assumptions are rubbish), proof of godhood.
First, assumptions:
Santa exists. He delivers, or attempts to, presents to young persons in the dark hours of Christmas Eve, while his target customers are asleep.
Santa delivers using a sleigh pulled by reindeer. Santa perhaps has ‘little helpers’, called elves.
A visit is supposed to include the following: sleigh arrives at house, Santa goes down chimney, delivers present to appropriate site, collects sherry, mince pie and carrot for his reindeer, departure.
Data and secondary assumptions:
There are two billion people of the right age group on the planet. Secondary assumption is that Santa is a ‘Christian’ notion (see here), so this reduces to between 350 and 400 million. The modelling I found suggests that this implies some 108 million households. I suggest that the single child households represent a bigger delivery problem, but will work with 100 million households, with an idea that twice as much might apply.
Delivering in the dark hours and using the time zones constructively gives Santa around 30 hours, maybe a little longer. He could begin at 19:00 one side of a dateline and end at 06:00 on the other side, but that range of hours, 33, implies that some age-groups are treated differently from others, which implies other assumptions over travel methods. So initially let us assume 30 hours (you may prefer to work with 24).
Assume, for the purposes of modelling, that households are the same size and that they are uniformly distributed over the globe. These two assumptions make the task easier, so the errors they introduce mean Santa must work faster than the implications of the assumptions. Assume all households behave the same way so that delivery can be efficiently distributed. These are dangerous assumptions, but they will establish a lower bound for behaviour and the tertiary assumptions that follow.
Let us look solely at travel issues for a while.
Reindeer as we know them cannot fly. Therefore our understanding of ‘reindeer’ is wrong and / or Santa’s reindeer are using high technology not generally available.
On the averaging basis assumed above, Santa, if working on his own, must reduce a ‘visit’ to around 1/1000th of a second [1.08 x108 households, 30x60x60 = 1.08x105 seconds => 10-3 seconds each], including travel between sites. The implications of this are boggling – more accurately, they cause us to reject some inherent assumptions. Ignoring other demands on the time, if there was only one delivery system, we are looking at nearly instantaneous travel that ignores issues of acceleration, momentum, resistances to motion and inertia. Putative engineers are expected to study this topic and can have useful fun exploring the consequences. For these folk, go visit here and produce for yourselves (and for your elves) the arguments generating the figures under the long third point. The exercise below contains a minimum number of points to explore.
Exercise, mainly mechanics:
1.1 If households are distributed uniformly, how is the mean distance between households 0.75 miles?
1.2 What is the lower bound for the mean speed of Santa’s sleigh (one sleigh only; zero time spent stopped)?
1.3 If the sleigh must stop at each household, produce a graph showing the balance between peak speed and accelerations required. Assume deceleration has the same absolute value as acceleration. Compare this with known values mankind can survive.
Conclusions include a subset of these ideas:
Santa is not alone. We recognise that a single source cannot do the deliveries within the bopunds set by the current assumptions.
Santa is not using delivery methods we can emulate at the moment. You might want to call this ‘magic’. For example, the accelerations alone required inertia-less travel. Again, we need to redefine some of our assumptions.
A brief excursion into the logistics of the presents provides other insights: if each present were 2lbs, says Dean Devlin ”Assuming that the average weight of presents Santa delivers to each child is 2 pounds, the sleigh is carrying 321,300 tons -- and that's not counting Santa himself, who, judging by all those familiar pictures, is no lightweight.” Assumption therein, that Santa starts with a full load. At 100 grammes each, we’re only ten times less; the sleigh suddenly has to be massive enough to carry 30 kilotonnes plus Santa and the reindeer, so think in terms of a large aircraft, not a dinky one-horse open sled scaled up a tad.
If Santa is not alone, how might his elves help? Do we dare assume that the ‘customers’ would insist on a Santa image doing the delivery? How many copies of Santa are manageable? Of course, the over 25s know the answer to this point and questions of this class and the knowledge spoils the whole concept of Santa. So, in a sweeping gesture, we will ignore it henceforth. Those (sensible folk) who draw decision trees for their models can add a line going from this decision diamond directly to the Stop circle icon (see diagram added at foot of the page). We are also close to denying our primary assumption (Santa exists), which is unacceptable.
Therefore we either reject our principal assumnption that Santa exists or we accept that Santa is not using delivery methods we can emulate at the moment. Or something else, because the assumptions are still incorrect. So what methods could be employed? Just because we don’t have such systems working does not mean that we cannot imagine them.
How about Star Trek style transporters? Observed cycle time in the programmes is around ten seconds per delivery, plus the time for the logistical loading and unloading, at least double that. Now we’re contemplating huge issues over locating sites, queueing presents in the vicinity of the transporter, collecting sherry / mince pie / carrot, identifying presents for Santa, etc, but even at 20 seconds each, we will need 20,000 transporters to cope with the 1/1000th of a second calculated earlier. On the other hand, we have removed the travelling problems at a stroke, losing all those mechanics issues and keeping the logistical ones. So the Star Trek model requires tens of thousands of transporters. That makes the ‘sleigh’ large: if there was only one and if transmission was from orbit, even a105 m³ vessel (Santa’s Sleigh) is ten miles in diameter. Now we’re talking Klingon ‘cloak’ technology too. You might like this different approach.
Exercise 2, mainly logistics:
2.1 Assuming a lot of automation, what multiplier of the volume of ‘presents’ is required for storage? Even if the same space could be re-used for storage of the offerings in the opposite direction, what delay (time offset) is reasonable? What volumes are being transported per time unit?
2.2 How much information is required to be held, of location (address), labelling, packaging, identification? Can you put a size to the storage required for the information? Can you identify how large this problem is by current standards? Do we need to contemplate several jumps in information technology to handle this traffic? Is there any merit in comparing this with air traffic control equivalents?
2.3 How would you go about setting up patterns for delivery? Can you see any advantage, given a matter transmitter, in there being a systematic approach? Turning that around, do you still need to apportion work geographically?
2.4 What are the mechanical effects on an orbit of rapid mass transfer? Suppose there is no exchange and only delivery; what effect does a decrease in mass have on a satellite? If you accept that exchange occurs, what are the subsequent effects of mass change? What sort of controls are required to balance this? Assume that the range at which a matter-mitter works is sufficiently narrow to require your attention.
2.5 Taking this issue alone, what is the effect on the orbit of Santa’s Sleigh when 300,000 tonnes of matter have left it? Assume no effort is made to counter the change in mass or change in orbit - just let it happen, and comment.
In Assembly, I suggested a reasonably manageable experiment. Many of my students came from affluent families and would have such things as a video camera available. What I suggested was that the camera be set up, a little covertly perhaps, so as to cover the site of the sherry, mince pie and carrot as previously mentioned. Now, if Santa is delivering personally, all the calculations we have done say the poor guy, for all that he apparently only ‘works’ one day a year, is moving very rapidly. Moreover, if he is going as quickly as we think, he has real problems just picking up the mince pie; his hand speed must slow down to close to zero to collect the pastry or the mince pie will disintegrate. Indeed his hand needs serious protection too. At a thousandth of a second per visit, I don’t think the collection can be by hand at all. So, I was hoping someone might capture an image of the hand taking the friendly food offering. Just two such images of the hand would establish the use of elves or not; valuable data for our modelling.
Of course the cynics in the Upper School might say they expect Santa’s hand to look very like that of a parent, conflicting perhaps with Assumption One. Many children would have great difficulty if Santa’s hand looked feminine (and why not? If someone can argue that Christ might have been female, why not Santa?) – judging by their faces in Assembly, this was very much a step too far. Little sexist beasts; why can’t elves be female, or just look female? We had little agreement over which was more at risk, the mince pie or the sherry glass. The glass must be emptied and put back in place without being broken; I think it is acceleration that is the problem.
Exercise 3; further investigation
3.1 How fast can (i) pastry, food in general (ii) crockery, glass in particular, be accelerated? What equivalents do you think might be acceptable?
3.2 What are the implications of ‘drinking’ a small sherry inside a thousandth of a second? Is gravity relevant? What mechanisms are required to transfer a small amount of liquid from a delicate receptacle?
For some, the last exercise tells us that the 1/1000th of a second for a visit is too short, because the implications are such that the offerings simply cannot be handled. This is odd; the consequences of the politeness (generosity, civility, call it what you will) of the Christmas spirit renders invalid some of the earlier assumptions. If we require Santa to take as little as a second to take the offering, we are looking at 3 orders of magnitude increase in the time required……
Now suddenly we have made unexpected progress: we do not have enough seconds to service the 100 million homes [108 million seconds = 30 000 hours]. So Santa can’t do this on his own, or we have missed some implications. Could Santa be using time travel? Thirty thousand hours is more seconds than there are in a single year; Santa certainly can’t be doing this on his own.
A mince pie told you that much !!
DJS 20100112
I am puzzled that the diagram is not visible on a Google search. I found a version on the MEI website and took a screenshot from the 2013 specification.
Please note that the first assumption, that Santa exists, should not damage belief in Santa. Amazing, therefore, how often I was accused of doing exactly that. I think I prove that what happens is magic, not the reverse. perhaps some of the children exhibit evidence that thinking about anything at all, such as Santa, causes a level of rejection of concept. That might explain a whole load of teaching problems….