
A square is in 2-D and has 4 vertices, 4 edges, 2 diagonals and one face.
A cube is in 3-D, has 8 vertices, 12 edges, 16 diagonals (I counted them) and 6 faces.
What happens if we consider more dimensions? We can't draw them at all well and generally we have a limitation of reperesenting N dimensions in N-1 dimensions. You can sort-of draw a 4-D cube by drawing a small cube inside a larger one and connecting the corresponding corners. This is called a Schlegel diagram and the 4-D cube is called a tesseract.
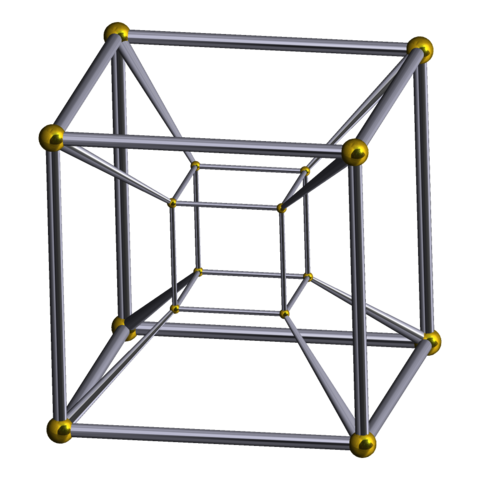
So let us use n for dimension, v for vertices and see if we can predict the vertices, edges, faces and diagonals for larger dimension.
Vertices: square, 2-D, 4; cube 3-D, 8; it seems clear that a 4-D cube will have 16 vertices and that v=2ⁿ.
Edges: To count edges, each vertex is joined to n other vertices —in the square, two and in the cube, three. This is like counting matches in a team game tournament, it takes two teams or vertices to make an edge. So the total number of edges is v.n/2 = 2ⁿ.n/2 = 2ⁿ⁻¹.n
Diagonals: To count diagonals in a square, we connect each vertex to every other vertex (and divide by two) and then subtract the number of edges because we've already counted those. You might check the diagonals on a cube to be sure I have this right. There are 8 vertices in a 3-D cube and, to make the diagonals and edges, each vertex is connected to 7 others, making 28 (diagonals plus edges). If we agree that there are 12 edges on a cube, then there must be 16 diagonals.
So edges + diagonals = v(v-1)/2 = 2ⁿ.(2ⁿ-1)/2 = 2ⁿ⁻¹(2ⁿ-1) which makes
diagonals = 2ⁿ⁻¹(2ⁿ-1) - 2ⁿ⁻¹.n = 2ⁿ⁻¹(2ⁿ-n-1) You should just check this works for the two samples we have.
The concept of a face on a tesseract is quite hard to visualise, but you might agree that there are eight 'cubical' shells, each bounded by twelve edges. In the same way a cube unfolds into six squares to form its net. So 4-D, eight cubes; 3-D 6 faces, 2-D 4 edges. This might be simply twice the number of dimensions, so that a n-cube has 2n facets of dimension n-1. I think this makes a lot of sense. We can check this by looking at the 1-dimensional case, which we have so far avoided thinking about. The 1-D 'cube' is a piece of straight line, with two endpoints; the square has four edges (each a line segment, a 1-D cube); the cube has 6 squares as faces; the tesseract has eight 3-D cubes as its facets.
With this idea of relating the next hypercube to the last one we are then happy (or even happier) that the number of vertices is 2ⁿ
A long time spent staring at the 4-cube, the tesseract, shows it has 8 cubes, 24 squares, 32 edges and 16 vertices. That is, the 4-cube contains 8 3-cubes, 24 2-cubes 32 1-cubes and 16 0-cubes. You see these in the column headed 4 below. I played with the numbers for a while before I found a formula. If we were to call these the R-cubes inside an N-cube, then I see a formula, 2ᴺ⁻ᴿ ᴺCᵣ.
The nCr function on the calculator is achieved with the COMBIN(n,r) function in Excel.
I discovered that the 4-cube, the tesseract can be called a regular octachoron (in the same way that a cube is a regular hexahedron); that a 5-cube is a penteract and a regular decateron; in consequence a 6-cube is presumably a hexeract, followed by hepteract, octeract, etcetera.
Having scribbled some figures down, I think the triangular series point, line, equilateral triangle, tetrahedron, etc has an equivalent table where the entries are, simply, n+1 C r +1, as above. Apparently, each member of this series is called a regular simplex (with dispute over the plural form of the word, simplexes or simplices). Thus the 3-simplex is a regular tetrahedron, the 4-simplex is a regular pentachoron, the 5-simplex a regular hexateron — I'm sure you get the idea.
We need some new words for these higher dimension shapes.
Definition: A polytope is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces(polygons), and cells(polyhedra). Each face is shared by exactly two cells. wikipedia
Definitions you might look up: convex polytope, regular polytope, semiregular polytope, uiniform polytope, scaliform polytope, prismatic polytope.
The words connected and closed ought to have good definitions, but (i) I found both difficult to express clearly and (ii) we're dealing with a subset, the regular polytopes, where each cell is also a regular polytope, so we can duck out of needing such a definition.
The five regular solids—the Platonic solids—mentioned at school (in the UK) are the tetrahedron, the cube, octahedron, dodecahedron and iscosahedron. The word regular is used to indicate that all the faces are the same shape and size. We can classify these (I did, at primary school age) by identifying the edges to each face and the edges at each vertex. So the Platonic solids in the same order are {3,3}, {4,3}, {3,4}, {5,3} and {3,5}, which means that there is a sense in which {p,q} will be equivalent to {q,p}, somehow finding meaning in swapping edges for faces. Or, in the case of 2-D shapes, swapping vertices for edges. Such a swap causes each pair to be called duals. In higher dimensions, the dual is found by writing the Schläfli symbol {.....} backwards, so that {p,q,r} is the dual of {r,q,p}. Hence, you will recognise that a palindromic Schläfli symbol is its self-dual.
Later (younger) students than myself might have come across Schläfli symbols, any of which is a list such that a 6-dimensional regular polytope is represented by {p,q,r,s,t} (length one less than the dimension) and the list is of facets (the t shapes {p,q,r,s}) around each peak of dimension t. So any regular polytope {p,q,r,s,t} has t {p,q,r,s} facets around each peak. Thus in a polyhedron (3-D) a facet is a face (2-D) and a peak is a vertex (1-D); in a 4-D polytope, the 3-D facets are polyhedra (cells), the 2-D peaks are edges.
If you recognise any sort of star (★, ✶) as a regular figure, the Schläfli symbol (in 2-D, so a single figure) looks like an improper fraction and the two I've implied but not drawn properly are {5/2} and {6/2}; the first number is the vertices and the second number is the count of vertices skipped when drawing the figure. You might recognise that {5/3} = {5/2} and draw for yourself the set {9/2}, {9,3}, {9,4}.

I'll tell you that there are nine regualr polyhedra: A regular polyhedron having faces {n} with p faces joining around a vertex is denoted by {n, p}. The nine regular polyhedra are {3, 3} {3, 4} {4, 3} {3, 5} {5, 3} {3, 5/2} {5/2, 3} {5, 5/2} and {5/2, 5}. {p} is the vertex figure of the polyhedron. You can draw them yourself from this.
The tetrahedron is in three dimensions and had four faces; as such it is a very simple shape and could be called, as explained above, the regular 3-simplex. When we move up to four dimensions, the 4-simplex (image above right) is named for its five cells; five regular, tetrahedral, 3-simplex, cells. Its other names are pentachoron, pentatope, pentahedroid and the regular 5-cell. It's Schläfli symbol is {3,3,3}. Wikipedia confirms my 4th column (5,10,10,5) above in the simplex table.
Thinking of regular 4-D polytopes (and rejecting the star equivalents, so only the convex polytopes), I think we might have {3,3,3}, {3,3,4}, {4,3,3}, {3,4,3}, {5,3,3}, {3,3,5}, and perhaps {3,5,3} as regular 4-polytopes. I see that John Conway (who I met at breakfast at college twice) has played with this mathematics. I'll tell you that of my seven suggestions, one is wrong.
Why is {3,5,3} not a regular polytope? Because it would be its self-dual. Each vertex has three edges, each edge has five faces (can that be done?) and each face has three tetrahedra.